2. 中国科学院地理科学与资源研究所, 北京 100101
2. Institute of geographic sciences and resources, Chinese academy of sciences, Beijing 100101, China
党的十九大报告把污染防治作为决胜全面建成小康社会的三大攻坚战之一,提出构建以政府为主导、企业为主体的环境治理体系,落实企业环境治理主体责任重大战略任务。排污者是污染治理的责任主体,强化其环保责任有助于改善环境质量,推动形成规范公平的市场竞争环境。中央政府制定了一系列的法律、法规来防治工业污染,如《中华人民共和国固体废物污染环境防治法》《中华人民共和国水污染防治法》《中华人民共和国大气污染防治法》等,规定各方在生态环境保护、污染防治等领域全方位开展工作;我国现行有效的国家污染物排放(控制)标准达160余项,对重点地区重点行业执行更加严格的污染物排放限值,在促进技术创新和推动企业升级改造方面发挥了重要作用。地方政府要根据改善环境质量的需要和经济、技术条件制定切实措施达到污染物排放目标;而环境保护如何与地方产业协调发展,是地方政府面临的突出问题。地方政府寄希望于企业自主提高环境意识,自我环境约束达到国家排放标准目标还面临诸多问题。应规定企业对其产生的污染要承担的责任和义务,以及采取切实可行的奖惩措施,督促企业完成“三废”治理工作,切实做到外部成本内部化。地方政府该如何制定奖惩措施,才能既使企业的排污工作达到环境标准,又不影响企业的生产积极性?本文将尝试建立政府和企业之间的双层优化环境治理模型,研究地方政府加强环境管理,督促企业积极改善污染排放的可行方案。
区域环境问题的政企博弈在主导产业重工业化特征明显、企业长期粗放式生产排污严重、地方政府环境监管有待加强、西北生态安全屏障和黄河流域健康发展受到严重威胁的宁蒙沿黄地带表现典型[1-6],部分文献对重污染产业区企业污染问题进行了研究[7-18],但很多是对企业的污染行为进行分析,强有力的环境管治措施研究有待加强,尤其缺乏数理推导研究。发达国家企业对其产生的污染责任明晰,尤其是ISO14001环境标准颁布后,企业相继加入环境认证。但很多企业环境责任承担严重不足,也没有考虑加入ISO14001体系,环境管理一直处于滞后状态,很多企业为了节省成本将“三废”直接排放,我国以宁蒙沿黄地带为代表的广大西北地区尤为典型。经调研发现,出现污染事故的企业大多都清楚超标排放污染物属违规行为,也清楚工业垃圾对环境的危害,更知道该如何避免或减少环境污染。但是处理“三废”不但需要购买各种过滤、净化设备以及改进技术等,还需要租用场所、培训工人等,增加企业支出,很多企业为了降低生产成本而不愿治理[19]。双层规划法(主从决策法)在20世纪70年代由Chandler和Norton等人最早提出,双层规划法考虑了决策过程中不同决策者(上层和下层,又称领导与随从)的作用和表现,现在已被广泛地应用于经济管理、金融、交通、环境保护等领域。近些年,一些学者开始关注环保问题,借助双层优化环境治理模型来探讨实际生产中,如何让企业在追求经济效益的同时主动保护环境,如基于环境保护的双层优化选址模型[20]、产品回收再生产的闭环双层物流模型[21]等。目前用双层优化方法来探索地方政府如何制定奖惩措施来督促企业排污达标的研究还有待完善,尤其西北重污染区相关研究较为缺乏。本研究将建立以地方政府为上层、企业(尤其重污染企业)为下层的双层优化环境治理模型,讨论上层地方政府如何制定奖惩措施和污染税费比例,能使下层企业在追求经济利益的同时主动治理其产生的污染,达到环境治理目标。首先,基于地方政府决策变量与企业决策变量,确定上层—下层目标函数及约束条件,建立地方政府与企业之间关于治理废水、废气和废渣的双层优化环境治理模型,研究地方政府环境奖罚政策与企业利润及环境行为的关联性;然后,给出模型解的存在性条件,提出模型“乐观最优解”与“悲观最优解”及地方政府奖惩机制最优解;最后,进一步分析政府的环境治理奖惩方式和税费比例对企业利润及环境行为的影响,并进行政策讨论,以期为宁蒙沿黄地带及类似地区强化排污者责任、实现国家排放标准目标、实现环境经济协调可持续发展提供参考。
1 宁蒙沿黄地带环境污染状况宁蒙沿黄地带是我国西北老工业基地和典型资源型城市的集聚区域,是我国西北乃至整个西部的重要增长极[1],基本形成了以能源、建材、冶金、装备制造业等为主导的重化工业体系,宁东能源重化工基地和陕北新兴能源重化工基地,也是我国“西煤东运”“西气东输”“西电东送”的重要基地之一[2, 3]。宁蒙沿黄地带总体处于工业化初中期阶段,二产比重60%左右,重工业比重在80%以上,而三产比重低,很多企业采用的是能耗高、污染重、资源利用率低的传统生产模式,给当地本来就脆弱的生态系统带来了巨大压力,如近20年内蒙古乌海、阿拉善、鄂尔多斯等地在黄河两岸数十公里的狭长地带开设工业园区,且多以高能耗、高污染的企业为引进对象,对黄河的环境安全产生了严重影响。在沿黄地区经过合理处理处置的城市垃圾、工业垃圾比重不到10%,饮用水源、大气环境影响着3/4以上的居民[4]。宁蒙沿黄地带成为我国环境污染最为突出的区域[1-5],单位工业产值“三废”排放量,特别是大气污染排放量远高于全国平均水平,污染治理水平有待提高。地方政府环境规制失位、监管不力是区域环境问题的重要原因。①废水污染,主要来自化工、冶金、有色金属等行业。近20年黄河排污量增加了1倍,干流近40%的河段水体功能影响严重。从青海经甘肃、宁夏至内蒙古的黄河沿岸,能源、重化工、有色金属、造纸等高污染工业废水排放量逐年增大[5]。②大气污染,主要来自燃料燃烧和工业生产过程。前者污染物主要为颗粒物、硫氧化物和氮氧化物等,涉及火电、钢铁、焦化等行业;后者污染物主要有粉尘、含硫化合物、VOC、含氮化合物以及卤素化合物等,涉及化工、石化、钢铁、水泥等行业。沿黄地区工业SO2排放量仍是全国平均水平的2倍左右。在2018年全国空气污染城市排名中,石嘴山、包头、兰州、银川、呼和浩特等沿黄城市的污染程度均在前列。③固体废弃物污染, 主要包括矿山尾矿、粉煤灰、锅炉渣、冶炼废渣等。很多工业垃圾未经处理直接排放,直接威胁生态系统安全[6]。
2 企业治理“三废”优化模型针对废水排放,设




设地方政府决策变量为



|
其中,y1, y2, y3分别表示企业每月治理废水、废气和废渣的量,是企业决策变量;







|
约束条件表示地方政府对企业的处罚金额是非负的(政府的处罚不能高于某个企业所能接受的最大数值);税收比例介于0和1之间。
设企业只生产一种产品(多种产品同理),其决策变量为


|
其中,εixi中i=1,2,3表示企业每月产生的废水、废气和废渣的量(常量);εi中i=1,2,3表示总产量为x时产生的废水、废气和废渣的比例(常量);p,c分别表示该种产品的平均单位价格和平均单位成本(常量);(p-c) x表示企业生产该种产品的月平均利润。c1l(l=1, 2, …L)表示企业治理单位废水中第l种污染物的成本(常量);









|
其中,约束条件表示企业的月生产量非负且不超过月最大生产能力a(a是常量,由企业的生产能力决定);企业治理“三废”的量yi, i=1, 2, 3不超过每月产生“三废”的量εix;企业的生产成本cx和治理“三废”的成本
标记整个双层优化环境治理模型为(P),则由(P)可看出,地方政府每采取一个奖罚政策(z, u),企业会相应地给出使自己利润最大的生产、治理方案(x, y),依据该方案企业制定产量及污染治理对策。地方政府可根据企业的决策方案调整其奖惩力度,实现区域环境目标。
3 模型解的存在性以及两种特殊情形 3.1 解的存在性记双层优化环境治理模型(P)的可行集为:

|
满足上层规划约束条件,x,y满足下层规划约束条件。
上层的约束集为:

|
对于给定的上层变量(z, u),记下层可行解集为:

|
满足下层规划约束条件。
下层的约束集是非空有界凸多面体,也是闭集。而下层最优解集记为:
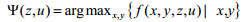
|
满足下层规划约束条件。这里Ψ(z, u)是点到集合映射。
引理1[20]:如果上层约束集W是非空紧集,对于每个给定的上层变量(z, u)∈W,下层至多有一个最优解,且可行集S非空,则双层优化问题(P)至少有一个最优解。
显然,适当选取参数,可保证双层优化问题(P)满足引理1所有条件,使该模型至少存在一个最优解。
3.2 两种特殊情形 3.2.1 乐观最优解乐观最优解是指上层领导者(地方政府)乐观地认为其有能力去影响下层(重污染企业)的行为,使得后者选择最利于上层目标函数的行动,此时求解模型得到的解为乐观最优解。
令函数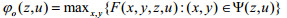
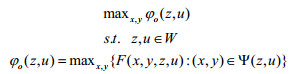
|
(P1) |
引理2[22]:对于乐观优化模型(P1),如果可行集S是非空紧集,下层问题在任何点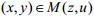
问题(P1)的全局最优解称为原双层优化问题(P)的全局乐观最优解,在此认为不论企业是积极采取措施治理污染还是在政府的强制措施下治理污染,都是一种与政府合作的态度,故视为“乐观”情形。
3.2.2 悲观最优解悲观最优解是指政府无法保证企业会按照自己期望的方式治理污染,此时求解模型得到的解称为悲观最优解。本文中悲观情形特指企业不愿治理污染,并将部分有危害的“三废”直接排放到外界环境中。
令函数
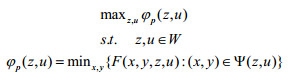
|
(P2) |
悲观优化模型(P2)不能保证有解,但是当下层最优解集Ψ(z, u)满足下半连续时,全局悲观最优解存在。
引理3[22]:对于悲观问题(P2),如果点到集映射Ψ(z)是下半连续的,且可行集S是非空紧集,则问题(P2)如果存在可行解,一定存在全局最优解。
问题(P2)的全局最优解称为原双层优化问题(P)的全局悲观最优解。这样不管是企业愿意与政府合作的乐观情形,还是不情愿合作的悲观情形,只要适当地调整模型的参数,就可以找到最优解。问题(P1)和(P2)是双层优化问题(P)的两个特殊情形,下面地方政府的奖惩及税费措施对企业决策及效益的影响分析将会说明这两种特殊情形的存在条件。而对于一般的双层优化问题(P),用于求解该类模型的有效算法比较多,如罚函数算法[22-24]、信赖域算法[25]、SQP算法[26]、SLP算法[27]等。在此利用间隙函数将其转化为单层模型后,采用罚函数方法求解。
设函数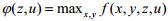
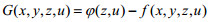
因此,双层优化问题(P)可以等价于下面的单层优化问题(P3)[22, 23, 27, 28]:
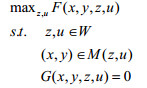
|
(P3) |
(P3)中约束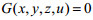
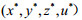
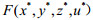
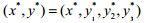
下面研究上层政府的处罚金额z对下层企业治理量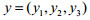
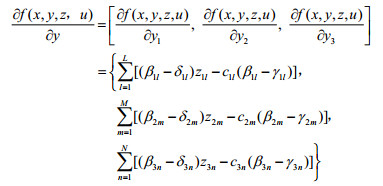
|
令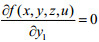
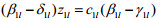
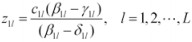
令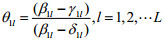
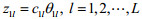
同理,令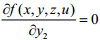
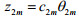
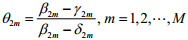
令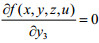
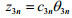
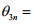
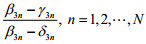
处罚
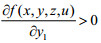
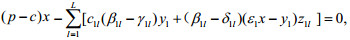

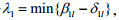
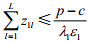
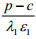
同理可分析z2m,z3n(m=1,2,…M,n=1,2,…,N)对下层目标函数的影响。为督促企业治理“三废”,政府的处罚值应该大于企业治理污染物的单位成本的θ倍,但不要超过给定的上限。
结论1:对于双层规划模型(P):
(1)当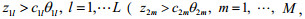
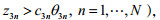
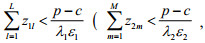

(2)当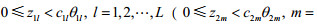
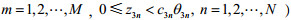
(3)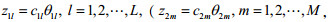
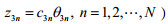
模型解第一种情形为乐观最优解。地方政府需要将处罚金额定在第一种情形的范围内。第二种情形此时模型的解为悲观最优解。第三种情形中,如果政府不能劝说下层企业治理污染,政府的目标函数值有可能达到最小值零。
4.2 地方政府征收的污染税费比例ui(i=1, 2, 3)对企业治理效果的影响
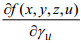
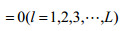
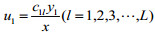
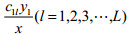
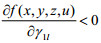
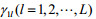
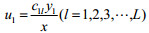
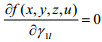
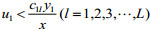
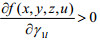
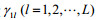
结论2:地方政府制定的污染税费比例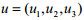
(1)当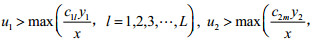
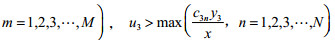
(2)当
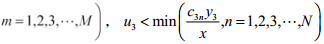
(3)当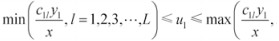
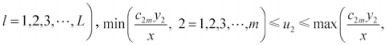
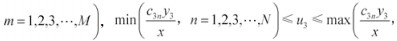
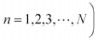
对于企业治理“三废”,地方政府给予的污染税费的比例不同,企业会有不同的决策反应。当污染费用的比例大过某个数值时,企业治理效果越好,利润越高,自然会积极提高其“三废”治理水平;而当污染费用的比例小过某个数值时,企业治理效果越好,利润越低,此时企业不愿意提高治理效果;当污染税费比例在某个范围内变动时,企业治理效果不对其利润产生影响,此时企业可以选择治理达标或者不达标。
5 结论污染防治是决胜全面建成小康社会的三大攻坚战之一。在我国环境法规与行业标准日益健全的情况下,如何加强地方政府环境监管,协调地方环境—经济效益至为关键。我国很多重污染区,包括西北宁蒙沿黄地区双高企业“三废”排放严重影响区域生态环境安全,严重制约区域协调可持续发展及沿黄战略性生态屏障建设;而地方政府环境管理缺位,尤其需要切实可行的奖惩机制来促使企业排污达到国家标准。如何制定奖惩标准是关键所在。为此,本研究建立了以地方政府为上层、企业为下层的双层优化环境治理模型,促使企业经济效益与环境效益共举,能够较为合理、可行地反映区域地方政府与企业的博弈过程。除了国家污染物排放标准(常数)外,模型其余参数均决定于地方企业,虽然不同企业的生产成本和排污技术水平不同,但对于每一企业在一定时期内给定的其他条件不变时其参数值与技术工艺水平关联可视为常量。对于宁蒙沿黄地区重污染企业,可应用此模型来探索督促企业“三废”治理工作,地方政府可根据不同企业类型制定不同的奖惩标准和污染税费比例,对于企业“三废”处罚金额要定在企业治理该污染物单位成本θ倍以上;而对于企业治理“三废”部分,地方政府可将污染税费比例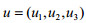
| [1] |
董锁成, 李雪, 石广义, 等. 宁蒙陕甘沿黄生态经济带建设构想[J]. 地理研究, 2010, 29(2): 204-213. |
| [2] |
王菲, 董锁成, 毛琦梁, 等. 宁蒙沿黄地带产业结构的环境污染特征演变分析[J]. 资源科学, 2014, 36(3): 620-631. |
| [3] |
樊正德, 赵锋. 我国西部能源"金三角"区域构建合作机制的模型分析[J]. 经济研究参考, 2018(41): 74-80. |
| [4] |
王菲, 毛琦梁. 工业结构与环境质量耦合优化情景模拟与策略——以宁蒙沿黄地带为例[J]. 生态经济, 2016, 32(1): 14-21. DOI:10.3969/j.issn.1671-4407.2016.01.004 |
| [5] |
李俊, 董锁成, 毛琦梁, 等. 宁蒙沿黄地带城镇用地变化及其生态效应[J]. 干旱区研究, 2016, 33(6): 1262-1269. |
| [6] |
仲俊涛, 米文宝, 候景伟, 等. 改革开放以来宁夏区域差异与空间格局研究——基于人口、经济和粮食重心的演变特征及耦合关系[J]. 经济地理, 2014, 34(5): 14-20, 47-47. |
| [7] |
黄秋森, 赵岩, 许新宜, 等. 基于弹簧模型的资源环境承载力评价及应用——以内蒙古自治区陈巴尔虎旗为例[J]. 自然资源学报, 2018, 33(1): 173-184. |
| [8] |
赵丽霞, 谭超. 内蒙古资源环境要素对经济增长的影响路径研究[J]. 干旱区资源与环境, 2017, 31(4): 16-21. |
| [9] |
宋林, 张杨, 郭玉晶. 环境约束下陕西城镇化效率的区域差异及空间格局[J]. 人文地理, 2016, 31(6): 115-122. |
| [10] |
张晓华, 杨庆, 马岩红. 甘肃部分农村窖水微生物污染状况调查[J]. 干旱区资源与环境, 2016, 30(5): 85-91. |
| [11] |
甄江红, 李灵敏, 何孙鹏, 等. 内蒙古工业化进程中的生态环境影响及其响应研究[J]. 干旱区资源与环境, 2015, 29(11): 86-92. |
| [12] |
宋敏, 郭清卉. 基于低碳视角的陕西能源消费与环境污染的灰色关联度研究[J]. 科技管理研究, 2015, 35(16): 243-247, 262-262. DOI:10.3969/j.issn.1000-7695.2015.16.045 |
| [13] |
胡振通, 孔德帅, 焦金寿, 等. 草场流转的生态环境效率——基于内蒙古甘肃两省份的实证研究[J]. 农业经济问题, 2014, 35(6): 90-97. |
| [14] |
万永坤, 董锁成, 毛琦梁, 等. 产业结构视角下的环境污染成因分析——以甘肃为例(英文)[J]. 资源与生态学报(英文版), 2013, 4(1): 88-92. |
| [15] |
王春萍, 吴媚. 西北地区人口-经济-环境耦合协调度评价——以甘肃庆阳为例[J]. 青海社会科学, 2012(5): 41-45. DOI:10.3969/j.issn.1001-2338.2012.05.011 |
| [16] |
邬亮, 马丽, 齐晔. 省级政府环境政策制定过程的特征分析——以陕西和云南水土保持生态补偿政策为例[J]. 中国人口·资源与环境, 2012, 22(3): 87-92. DOI:10.3969/j.issn.1002-2104.2012.03.015 |
| [17] |
王彦丽. 渭河流域陕西段水环境质量综合评价与对策研究[J]. 干旱区资源与环境, 2011, 25(11): 34-38. |
| [18] |
张智渊, 黄翔. 农用地膜的污染现状与对策探讨——以甘肃省通渭县为例[J]. 农业环境与发展, 2010, 27(6): 12-16. DOI:10.3969/j.issn.1005-4944.2010.06.003 |
| [19] |
李远方.巨资兴建的污水处理厂竟直排废水[N].中国商报, 2013-03-05.
|
| [20] |
胡长英, 刘国山. 基于环境角度的双层选址优化模型[J]. 中国管理科学, 2007, 15(4): 59-62. DOI:10.3321/j.issn:1003-207x.2007.04.009 |
| [21] |
胡长英. 逆向物流闭环双层优化模型及算法[J]. 运筹与管理, 2009, 16(3): 26-30. DOI:10.3969/j.issn.1007-3221.2009.03.005 |
| [22] |
DEMPE S. Foundations of Bilevel Programming[M]. US: Kluwer Academic Publishers, 2010.
|
| [23] |
HU C Y. Exactness of penalty functions for solving MPEC model of the transportation network optimization problems with user equilibrium constraints[C]//International Conference on Management Science and Engineering. Lille, France: IEEE, 2006.
|
| [24] |
LIU G S, HAN J Y, ZHANG J Z. Exact penalty functions for convex bilevel programming problems[J]. Journal of optimization theory and applications, 2001, 110(3): 621-643. DOI:10.1023/A:1017592429235 |
| [25] |
FLORIAN M, CHEN Y. A coordinate descent method for the Bi-level O-D matrix adjustment problem[J]. International transactions in operational research, 1995, 2(2): 165-179. |
| [26] |
CLEGG J, SMITH M, XIANG Y L, et al. Bilevel programming applied to optimising urban transportation[J]. Transportation research part B:methodological, 2001, 35(1): 41-70. DOI:10.1016/S0191-2615(00)00018-7 |
| [27] |
MENG Q, YANG H, BELL M G H. An equivalent continuously differentiable model and a locally convergent algorithm for the continuous network design problem[J]. Transportation research part B:methodological, 2001, 35(1): 83-105. DOI:10.1016/S0191-2615(00)00016-3 |
| [28] |
BROTCORNE L, LABBÉ M, MARCOTTE P, et al. A bilevel model and solution algorithm for a freight tariff-setting problem[J]. Transportation science, 2000, 34(3): 289-302. DOI:10.1287/trsc.34.3.289.12299 |
 2019, Vol. 11
2019, Vol. 11


