2. 城市绿色发展科技战略研究北京市重点实验室, 北京 100089
2. Beijing Key Laboratory of Study on SCI-TECH Strategy Urban Green Development, Beijing 100089, China
我国是一个水资源短缺的国家,人均水资源仅为世界平均水平的1/4。随着经济增长和城市化进程的加快,我国水资源供需矛盾日益突出。据相关专家估计,到2030年我国的缺水量将达到600亿m3 [1]。在此背景下,习近平总书记强调节约资源是保护生态环境的根本之策,要加大资源节约力度,集约利用资源,推动资源利用方式根本转变,加强全过程节约管理,大幅降低能源、水、土地消耗强度,尤其是要加强水源地保护和用水总量管理,推进水循环利用,建设节水型社会。
引言水价是调节水资源配置的重要经济杠杆,政府可以通过制定合理的水价政策影响企业的用水成本,从而促进企业节约用水,因此水价成为政府提高用水效率的重要政策工具[2]。当前我国水资源浪费仍然较为严重,用水效率远低于其他发达国家,许多学者认为主要原因在于当前水价太低,建议通过提高水价来促进用水企业节约用水,提高用水效率[3, 4]。但仍有许多地方政府和供水企业并没有提高水价,如天津、河北和山西等地的工业与经营服务业水价近几年呈下降的趋势(图 1)。为什么许多地方政府和供水企业在水资源短缺和用水效率较低的背景下没有提高水价,而是降低了水价?本文从博弈论的角度研究该问题,认为供水企业的水价决策与用水企业的节水策略是相互影响的(图 2),一方面,我国水价主要经供水企业与各级水行政主管部门、价格和财政等相关部门共同协商后由各级政府批准决定[5],因此供水企业在制定水价时既要考虑自身收益又要考虑公共福利,同时其水价策略又直接影响用水企业的用水成本,进而影响用水企业的节水策略;另一方面,各地用水企业在做出节水决策时主要考虑自身收益,用水企业的节水不仅可以减少自身用水成本,还为社会带来公共福利,包括社会效益和环境效益[6],后者正是供水企业追求的目标之一,因此用水企业的节水策略又会影响供水企业的水价决策。由此可见,供水企业的水价策略与企业的节水策略是相互影响、相互博弈的结果。与此同时,供水企业与用水企业是有限理性,并不能一次达到最优,而是经过数次博弈,双方不断学习,调整策略以实现各自利益的最大化,因此本文认为部分地区近年来持续低水价策略是各地供水企业与用水企业相互博弈演化的结果。

|
图 1 2007—2017年部分地区工业水价与经营服务业水价① 资料来源:中国水网 |
① 我国各地工业水价与经营服务业水价采用相同价格。

|
图 2 供水企业水价策略与用水企业节水策略关系 |
据此,本文采用演化博弈的分析方法通过构建供水企业与用水企业关于水价策略与节水策略的博弈模型,分析国内部分地区近年来持续实施低水价策略的原因,并进一步采用不完全信息动态博弈的分析方法,分析政府水务部门与供水企业在水价商议博弈中低水价产生的具体过程,对于理解某些地区实行低水价以及未来各地区建立节水型社会促进水资源节约具有指导意义。
1 文献综述本文从三个方面对当前关于水价政策的研究进行了梳理,目前主要是采用CGE模型②、博弈论和案例分析等方法研究水价政策对经济和水资源节约的影响。
② CGE(Computable General Equilibrium)又称可计算一般均衡,是以瓦尔拉斯一般均衡理论为基础,以一组数学方程的形式反映整个社会经济活动的数量经济模型,是一种政策分析模拟的工具。
(1)基于CGE模型的水价政策与节水关系研究。周芳和马中[7]以重庆市为例构建基于CGE模型模拟水价提升对经济、水资源节约和水环境的影响,通过模拟发现水价提升对GDP、居民收入、企业收入等经济指标确实会有负面影响,但是对水资源节约和水环境保护产生的收益更大。Zhao和Peng [8]采用加入总水量约束模块的SICGE模型模拟发现了类似的结论。王克强等[9]基于CGE模型对农业水资源各项政策包括水价政策进行模拟分析发现,将农业水价提高1%,农用水资源需求降低0.163%,能够起到节约水资源的效果,但是农业部门与非农业部门产出都下降。王韬[10]基于11个部门CGE模型以及严冬[11]以北京市为例的CGE模型也得出了类似的结果,即水价提升对水资源节约有正面影响,但是对整个经济造成一定的损失,政府需要在两者之间做一个平衡。
(2)基于博弈论的水价政策分析。廖虎昌[12]将博弈论研究方法用于云南省的节水策略研究,通过构建政府与用户之间的博弈模型说明当水价低于单位节水效益时政府提高水价可以促进水资源节约。卢丽荣[13]通过构建再生水与自来水厂和火电厂之间的博弈模型分析发现在短期内水价上涨是把“双刃剑”,一方面增加企业用水负担,另一方面促进节水技术的推广;从长期来看,既可以提高企业的竞争力,又可以促进水资源节约,保护水环境。刘晓君[14]和周妍[15]构建了水务设施管理企业与政府之间的博弈模型,提出政府在确定水价时既要保证社会公众利益,又要使水务设施管理企业的投资所获得的回报等于该资源的机会成本。安丰东[16]构建了政府与自来水厂之间的博弈模型,分析了政府的水价策略与水厂投资策略的相互影响,发现在一次博弈情况下政府有激励供水企业投资时选择低水价从而导致供水企业亏损,而在重复博弈情况下,政府基于企业行为历史信息改变下一轮博弈策略,以促进政府与供水企业的合作。
(3)其他关于水价政策与节水关系的研究。刘晓君[17]基于扩展性支出系统模型,验证了陕西省阶梯水价调整可以促进水资源节约,而且收入中等偏上家庭平均节水量最大。李世祥等[18]采用案例分析了水价提升的节水效应、资源配置效应、环境效益和资源配置效应,认为水价必须考虑公共利益。倪红珍和王浩[19]基于投入产出价格模型以北京市为例模拟了各类水价调整对其他经济部门产品或服务价格和水费的影响,发现北京各类水价提高对居民、行政事业以及高用水服务业的价格影响较大,其中工商业水价变动对各部门水费影响最大,整体而言,水价提升不会对经济社会产生较大的波动,并建议提高水价,以促进节约用水。
从以上文献整理可以看出,对于水价政策的研究,主要集中于水价提升对经济以及水资源节约的影响,至少在短期内这两者间存在一个平衡。但是对于具体的决策机制缺乏清晰的描述,CGE模型模拟了水价提升对经济的冲击以及水量的节约,只是一种宏观描述,政府与用水企业之间关于水价提升与节水决策之间是如何相互影响的微观机制缺少详细的描述,博弈论方法相比CGE这种传统系统工程方法更加细致地描述了各方利益相关者的决策行为,而且可以在定量信息缺失时通过定性信息就解决利益相关者的冲突[20]。还有一些学者虽然也采用了博弈模型研究政府与供水企业的水价与节水博弈,但是一方面他们的模型设置忽略了政府提升水价对经济产生的冲击,另一方面只分析用水企业的节水收益对其节水决策的影响,没有分析政府水价策略对其节水决策的影响。而其他采用博弈方法分析水价影响的研究主要集中于水厂之间的博弈和水厂与政府之间的投资决策博弈,而且几乎所有的博弈模型都没有考虑政府水务部门与供水企业关于水价商议的分析。因此,本文致力于建立供水企业与用水企业、供水企业与政府水务部门之间的博弈,系统分析供水企业的水价决策与用水企业节水决策相互影响的过程,从博弈论角度解释低水价产生的原因,对促进水资源节约具有一定的指导意义,这是本文的创新之处。本文的不足之处在于由于相关变量(如节水投入成本、提高水价的经济冲击成本)数据难以估算,只停留在逻辑推演层面,没有做相应实证检验,这也是本文未来进一步探索的方向。与此同时,本文所研究的水价也只限于工业水价、经营服务业水价等生产性水价,而不包括生活水价和行政事业水价等非生产性水价。
2 基础模型构建与求解 2.1 基础模型假设与构建本文采用用水企业单位产出耗水减少量来衡量企业的节水行为,并用耗水系数α来表示,用水企业根据水价和节水成本决定是否采用节水技术,其耗水系数分别用α1、α2表示,其中α1>α2,分别表示用水企业的不节水和节水生产策略,P1和P2分别代表供水企业的低水价和高水价策略,其中P1 < P2。为了构建简洁又不偏离现实的博弈模型,根据现实情况做出如下假设:
假设1:用水企业追求企业收益最大化,供水企业追求企业收益与社会收益之和最大化。
假设2:以(不节水,低水价)策略组合为基准线,用水量减少可以带来正社会收益g(∆W),并假设收益函数g(∆W)为线性增函数,且g(∆W=0)=0;采用节水技术需要用水企业投入成本f (∆α),其中∆α=α1−α2,表示节水技术进步,且f′ > 0,表示节水技术越高,投入的成本越大;f′′ > 0,表示节水技术的边际成本递增,f(∆α=0)=0,表示在(不节水,低水价)策略组合的基准线情况下,节水技术投入成本为0。
假设3:当供水企业提高水价时,用水成本的上升会给当地经济带来一定的冲击,导致经济总产量下降,因此本文假设提高水价会给整个经济造成损失L(∆P),∆P=P2−P1,L′ > 0,表示水价提高越大,产生的冲击越大,L" < 0,表示水价变动产生的边际效应递减。
假设4:用水企业采用节水技术与否,除了用水成本和节水投入成本,生产所需的其他要素成本C不变。
假设5:用水企业以概率x采用不节水策略,以概率(1− x)采用节水策略,其中0 ≤x≤1;供水企业以概率y采用低水价策略,以概率(1 − y)采用高水价策略,其中0 ≤y≤ 1。
根据上述假设,可以计算用水企业与供水企业采取各种策略组合的收益:
设W1=α1Y1,W2=α2Y1,W3=α1Y2,W4=α2Y2分别表示(不节水,低水价)、(节水,低水价)、(不节水,高水价)和(节水,高水价)状态下的用水量,由于α1>α2,Y1>Y2,故W1>W2>W4,W1>W3>W4。如表 1所示。
| 表 1 用水企业与供水企业用水量 |
(1)当用水企业与供水企业采用策略组合(不节水,低水价)时,用水企业与供水企业的收益分别为:

|
即用水企业获得收益等于生产产品的产值Y减去用水成本P1W1和其他要素投入的成本C,而供水企业的收益主要是供水收益,也是用水企业的用水成本P1W1。本文以不节水为基准线,故用水企业节水设施投入成本在不节水时为0,用水企业减少的用水量产生社会收益为0,且供水企业选择低水价策略时对经济冲击产生的损失也为0。
(2)当用水企业与供水企业采用策略组合(节水,低水价)时,用水企业与供水企业的收益分别为:

|
即用水企业的收益在原有基础上再减去节水投入成本f (∆α),供水企业获取用水减少而产生的社会收益g(W1−W2)和供水企业收益P1W2。
(3)当用水企业与供水企业采用策略组合(不节水,高水价)时,用水企业与供水企业的收益分别为:

|
L(∆P)表示水价提高对经济产生的冲击,其中∆P= P1−P2,W1−W3表示相对于基准情况减少的用水量。
(4)当用水企业与供水企业采用策略组合(节水,高水价)时,用水企业与供水企业的收益分别为:

|
则用水企业与供水企业的博弈模型如表 2所示。
| 表 2 用水企业与供水企业博弈模型 |
构造用水企业和供水企业行为策略的复制者动态方程:
(1)设Uα1u表示用水企业采取“不节水”策略的期望收益,Uα2u表示用水企业采用“节水”策略的期望收益,Uu表示用水企业的平均期望收益,则:
用水企业采用“不节水”策略获得的期望收益为:

|
(1) |
用水企业采用“节水”策略获得的期望收益为:

|
(2) |
用水企业行为的平均期望收益为:

|
(3) |
用水企业的复制者动态方程为:

|
(4) |
当复制者动态方程稳定,即

|
(2)设UP1s为用水企业采用“低水价”策略的期望收益,UP2s为用水企业采用“高水价”策略的期望收益,Us表示供水企业的平均期望收益,则:
供水企业采用“低水价”策略获得的期望收益为:

|
(5) |
供水企业采用“高水价”策略获得的期望收益为:

|
(6) |
供水企业价格策略获得的平均期望收益为:

|
(7) |
供水企业价格策略的复制者动态方程为:

|
(8) |
当复制者动态方程稳定,即

|
综合上述式(1)与式(2)供水企业和用水企业的均衡点,可以得出,当0 < a < 1且0 < b < 1时,由供水企业和用水企业水价策略与节水策略行为组成的二维动力系统的均衡点(0, 0),(0, 1),(1, 0),(1, 1),(a, b)。
2.3 演化均衡稳定性分析令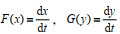

|
复制者动态方程的均衡点满足以下两个条件:

为了简化表达式并让经济含义更直观,做如下变换:
(1)设

(2)设

(3)设

则根据复制者动态方程稳定性条件可得表 3。
| 表 3 局部均衡点分析 |
依据表 3和复制者动态方程稳定条件,可以得到两个命题。
(1)命题1:当



|
图 1 用水企业与供水企业决策演化相位图 |
其经济含义是:①在高水价情况下,当用水企业采用节水技术增加的投入成本f(∆α)小于节水增加的收益∆π2,且在用水企业采用节水技术情况下,供水企业提高水价增加的私人供水收益∆z2与因水价提高而减少用水量增加的公共收益∆g2之和大于提高水价对经济产生的冲击L(∆P)时,用水企业与供水企业经过博弈最后可能会收敛到(0,0)均衡点,即(节水,高水价)策略组合。②在低水价情况下,当用水企业节水投入产生的成本f(∆α)大于节水增加的收益∆π1,且在用水企业采用不节水技术的情况下,供水企业提高水价增加的供水收益∆z1与因水价提高减少用水量而增加的公共收益∆g1之和大于提高水价对经济产生的冲击L(∆P)时,用水企业与供水企业经过博弈最后可能会收敛到(1,1)均衡点,即(不节水,低水价)策略组合。
供水企业与用水企业关于水价与节水的博弈最终可能会逐渐收敛到O(0,0)或B(1,1)策略组合的概率分别为:

|
(9) |

|
(10) |
由命题1可得到两个推论:
推论1:收敛到均衡点B(1,1)的概率PB与∆g2、∆z2、∆g1和∆z1成反比,与L(∆P)成正比。其经济含义是:供水企业提高水价增加私人供水收益与公共节水收益越小,则两者博弈收敛到(不节水,低水价)策略组合的概率越大;与此同时,提高水价对经济产生的冲击越大,博弈收敛到(不节水,低水价)策略组合的概率越大。
推论2:收敛到均衡点B(1,1)的概率PB与∆π2、∆π1成反比,与f(∆α)成正比。其经济含义是:用水企业由于采用节水技术而减少的用水成本越小,则两者博弈收敛到(不节水,低水价)策略组合的概率越大;而且采用节水技术的投入成本越大,则收敛到(不节水,低水价)策略组合的概率越大。
(2)命题2:当


|
图 2 用水企业与供水企业决策演化相位图 |
其经济含义是:①在高水价情况下,当用水企业采用节水技术增加的投入成本f(∆α)大于节水增加的收益∆π2,且在用水企业采用节水技术情况下,供水企业提高水价增加的私人供水收益∆z2与因水价提高而减少用水量增加的公共收益∆g2之和小于提高水价对经济产生的冲击L(∆P)时,用水企业与供水企业经过博弈最后可能会收敛到(0,1)均衡点,即(不节水,高水价)策略组合。②在低水价情况下,当用水企业节水投入产生的成本f(∆α)小于节水增加的收益∆π1,且在用水企业采用不节水技术情况下,供水企业提高水价增加的供水收益∆z1与因水价提高减少用水量而增加的公共收益∆g1之和大于提高水价对经济产生的冲击L(∆P)时,用水企业与供水企业经过博弈最后可能会收敛到(1,0)均衡点,即(节水,低水价)策略组合。根据现实情况,各地区出现(节水,低水价)或(不节水,高水价)策略组合的情况较少,因此本文并不对该命题进行进一步展开。
因此,综合上述命题和推论可以得出有些地区处于(不节水,低水价)的均衡状态的主要原因在于:供水企业提高水价对经济产生的冲击L(∆P)较大,而提高水价增加的私人供水收益与公共节水收益不足,从而导致有些地区供水企业不敢提高水价,一直采用低水价策略;与此同时,这些地区采用节水技术的投入成本f(∆α)较大,而增加的节水收益太小,从而导致用水企业采用不节水技术。
3 供水企业与政府水务部门水价商议博弈模型水价是由供水企业与政府水务部门一起商议决定的,因此供水企业不得不承担社会责任,在追求企业利益的同时又要兼顾公共利益,为了进一步说明低水价的产生过程,本节采用不完全信息动态博弈论的方法分析政府水务部门与供水企业关于水价商议的博弈模型。
3.1 模型假设与构建在基础模型的基础上,为了进一步研究供水企业与政府水务部门的水价商议过程,构建一个供水企业与政府水部门水价商议的动态博弈模型(表 4),为了描述现实又不失简洁,对该博弈模型做如下假设:
| 表 4 供水企业与政府水务部门水价商议博弈模型 |
假设6:供水企业与政府水务部门就水价的制定进行博弈,此时供水企业只追求企业收益最大化,而政府水务部门只追求公共收益最大化,即将基础博弈模型(表 2)中的供水企业角色拆分成政府与企业,不再是两者的综合体。
假设7:政府水务部门拒绝报价时,水价协议不能达成,双方收益为0,继续重复相同的博弈,不考虑时间贴现。
假设8:供水企业与政府水务部门在商议水价时都不知道在该水价情况下用水企业是节水还是不节水,只知道用水企业以概率q选择不节水,以(1-q)概率节水,而用水企业的节水概率分布是政府水务部门与供水企业的共同知识。根据假设6~8和供水企业的基础博弈,构建如表 4所示的供水企业与政府水务部门水价商议博弈模型的战略表达式。
(1)在用水企业不节水情况下,供水企业提议低水价,政府水务部门同意时,政府没有任何节水公共收益,此时政府水务部门收益Ug1 = 0,供水企业获得供水收益
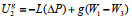

(2)在用水企业节水情况下,供水企业提议低水价,政府水务部门同意时,政府水务部门获得节水公共收益



(3)在政府水务部门拒绝供水企业报价的情况下,两者收益为0,然后重新开始相同的博弈,直到达成价格协议为止。
3.2 均衡求解与分析政府水务部门与供水企业构成了一个动态博弈模型,为了更好地求解该动态博弈,将表 4转换成扩展式博弈模型,如图 3所示。

|
图 3 供水企业与政府水务部门水价商议博弈模型扩展表达式 |
设政府水务部门采取“同意”策略获得的期望收益为Uag,采取“拒绝”策略获得的期望收益为Urg,供水企业提议低价获得期望收益UP1s,提议高价获取期望收益UP2s采用逆向归纳法求解:
3.2.1 政府水务部门决策当供水企业提议“低水价”时,政府水务部门“同意”的期望收益





当供水企业提议“低水价”时,由式(1)可知,政府水务部门会同意报价,此时供水企业会期望收益
当供水企业提议“高水价”,且p0 < q时,政府水务部门会拒绝报价,此时供水企业的期望收益UP2s(1)=0,由于UP1s(1)>UP2s(1),故供水企业会选择提议“低水价”,此时政府水务部门同意报价,即最后博弈的均衡结果为(低水价,同意)策略组合。
当供水企业提议“高水价”,且用水企业不节水概率p0 > q时,政府同意水务部门报价,此时供水企业的期望收益



综上所述,可得到命题3:当p0 < q时,供水企业与政府水务部门水价商议博弈的均衡结果为(低水价,同意);当p0 > q时,供水企业与政府水务部门水价商议博弈的均衡结果为(高水价,同意)策略组合。
进而产生推论3:p0与高水价对经济产生的冲击成本L成反比,与∆g1、g(W3-W4)成正比,即高水价对经济产生的冲击成本越大,且在不节水情况下高水价增加的公共收益越小,高水价情况下采用节水技术增加公共收益越小,则p0越小,政府水务部门与供水企业博弈结果为(低水价,同意)策略组合的可能性越大;反之,则达成(高水价,同意)策略组合博弈结果的可能性越大。该推论与供水企业和用水企业的博弈结论一致,进一步说明了低水价产生的过程。
4 主要结论及其相关讨论通过上述供水企业与用水企业、政府与供水企业博弈均衡结果的分析,本文可以得出以下结论:
(1)供水企业提高水价所增加的私人供水收益与公共节水收益越大,且提高水价对经济产生的冲击越小,两者博弈收敛到(不节水,低水价)策略组合的概率越小,收敛到(节水,高水价)策略组合的概率就越大。因此,政府水务部门在考虑通过高水价促进企业节约用水时,可以对用水企业进行相关优惠补贴或税收减免等各种配套的政策减缓水价提高带来的经济冲击。
(2)用水企业由于采用节水技术所减少的用水成本越大,采用节水技术的投入成本越小,则两者博弈收敛到(不节水,低水价)策略组合的概率越小,收敛到(节水,高水价)策略组合的概率越大。因此,政府水务部门为了促进企业节约用水不一定要采用高水价策略,可以对用水企业进行节水补贴来减少用水企业节水技术投入成本,以激励用水企业进行节水技术创新,引入国外先进节水技术,从而促进当地用水企业节约用水。
(3)在政府水务部门与供水企业在水价的商议过程中,高水价对经济产生的冲击成本越大,且在用水企业不采用节水技术情况下由于高水价导致企业用水量减少产生的公共收益越小,则政府水务部门与供水企业博弈结果为(低水价,同意)策略组合的可能性越大;在用水企业节水情况下提高水价政府水务部门增加的公共收益越大,同时供水企业采用节水技术增加的收益越小,则政府水务部门与供水企业博弈结果为(高水价,同意)策略组合的可能性越大。而当前某些地方政府不重视节水的长期公共收益,只重视短期经济收益时,会导致持续采用低水价政策,从而导致用水浪费。
与此同时,由于本文博弈模型构建在相关假设基础之上,本文的结论只在一定范围内成立,因此对本文的研究结论需要做出一定说明:
(1)本文所研究的水价主要指生产性水价,包括工业水价、经营服务业水价、特种行业等,不包括生活水价和行政事业水价等非生产性水价,也不包括农业水价。我国市场水价分5类:生活水价、工业水价、经营服务业水价、行政事业水价和特种行业水价,行政事业水价主要指政府机关和部队等公共事业单位用水价格,而农业水价通常以电价的形式收取,并没有单一的水价,因此也不考虑在内。
(2)供水企业在向政府就水价制定进行报价时,通常采用成本加部分利润的形式提议水价,如果供水成本下降,如因水网的固定成本被众多用户长期分担而导致供水成本下降,从而导致水价下降。供水成本的下降确实可能是造成低水价的原因之一,虽然在本文的模型构建中假设了供水成本不变,但是笔者认为供水企业与用水企业以及与政府水务部门的博弈也从另一个角度解释了低水价产生的原因,两者并不冲突。至于两者之中谁占主导需进一步分析。
(3)本文由于相关变量的真实数据(比如,供水企业的节水投入成本、高水价的经济冲击成本)难以获得,因此只有理论层面的逻辑推演,需要具体的数据进行实证检验,这也是未来需要进一步探索的方向。
| [1] |
苑韶峰. 水价及水资源节约问题探讨[J]. 价格理论与实践, 2008(2): 32-33. |
| [2] |
谢慧明, 强朦朦, 沈满洪. 中国工业水价结构性改革研究:水资源费的视角[J]. 浙江大学学报(人文社会科学版), 2018, 48(4): 54-73. |
| [3] |
刘静, 陆秋臻, 罗良国. "一提一补"水价改革节水效果研究[J]. 农业技术经济, 2018(4): 126-135. |
| [4] |
李太龙, 沈满洪. 促进工业节水的水价调控战略研究[J]. 河海大学学报(哲学社会科学版), 2015, 17(4): 82-88. |
| [5] |
刘世庆, 许英明. 我国城市水价机制与改革路径研究综述[J]. 经济学动态, 2012(1): 91-95. |
| [6] |
徐涛, 姚柳杨, 乔丹, 等. 节水灌溉技术社会生态效益评估——以石羊河下游民勤县为例[J]. 资源科学, 2016, 38(10): 1925-1934. |
| [7] |
周芳, 马中. 基于CGE模型的水价改革影响研究——以重庆市为例[J]. 中国地质大学学报(社会科学版), 2014, 14(1): 47-54. |
| [8] |
ZHAO J, NI H Z, PENG X J, et al. Impact of water price reform on water conservation and economic growth in China[J]. Economic analysis and policy, 2016, 51: 90-103. DOI:10.1016/j.eap.2016.06.003 |
| [9] |
王克强, 李国军, 刘红梅. 中国农业水资源政策一般均衡模拟分析[J]. 管理世界, 2011(9): 81-92. |
| [10] |
王韬, 叶文奇. 水价上涨、居民福利与水资源效用提升[J]. 改革, 2012(9): 143-151. |
| [11] |
严冬, 周建中, 王修贵. 利用CGE模型评价水价改革的影响力——以北京市为例[J]. 中国人口·资源与环境, 2007, 17(5): 70-74. |
| [12] |
廖虎昌, 董毅明. 基于博弈论的云南省水量定价模型[J]. 节水灌溉, 2010(10): 78-80. |
| [13] |
卢丽荣. 水价改革与节水技术推广的博弈[J]. 水利经济, 2011, 29(5): 31-33, 37. |
| [14] |
刘晓君, 李颖. 博弈论在城市水资源定价中的应用[J]. 河北工业大学学报, 2004, 33(4): 41-44. |
| [15] |
周妍, 郑立群. 水价制度与我国的水资源定价[J]. 内蒙古农业大学学报(社会科学版), 2007, 9(1): 101-103. |
| [16] |
安丰东. 中国城市自来水定价及厂商行为趋向研究[J]. 统计与决策, 2007(9): 52-53. |
| [17] |
刘晓君, 丁超. 城镇居民阶梯水价定价的合理性与有效性研究——基于陕西省水价数据的实证分析[J]. 价格理论与实践, 2012(7): 27-28. |
| [18] |
李世祥, 吴巧生, 刘爱新, 等. 武汉市水价上调的政策效应分析[J]. 经济理论与经济管理, 2005(9): 26-30. |
| [19] |
倪红珍, 王浩, 赵博, 等. 基于投入产出价格影响模型的水价调整影响[J]. 系统工程理论与实践, 2013, 33(2): 363-369. |
| [20] |
MADANI K. Game theory and water resources[J]. Journal of hydrology, 2010, 381(3-4): 225-238. DOI:10.1016/j.jhydrol.2009.11.045 |
| [21] |
BRAUN M. 微分方程及其应用(第四版)[M]. 北京: 世界图书出版公司, 2015.
|
 2019, Vol. 11
2019, Vol. 11






