2. 重庆大学经济与工商管理学院, 重庆 400030
2. School of Economics and Business Administration, Chongqing University, Chongqing 400030, China
水资源是人类赖以生存和发展的重要自然资源。我国《“十四五”节水型社会建设规划》明确指出,水资源严重短缺是我国的基本水情,是社会经济发展的重要瓶颈制约。全面提升水资源利用的效率和效益,是缓解我国水资源供需矛盾、保障用水安全的必然选择。我国河流虽然众多,但是分布不均,实行流域水资源跨区域配置可以改变水资源原有空间布局,缓解部分地区水资源供需矛盾,提高水资源综合利用效率 [1,2]。如何选择跨区合作的对象,如何处理公平与效率的关系,如何共享合作产生的收益,是水资源跨区配置迫切需要解决的难题。
目前学者们主要采用合作博弈解决此类问题。较早的研究主要是运用清晰联盟合作博弈。Wang等 [3,4]在流域用水部门之间建立两阶段水资源配置合作模型(CWAM),运用合作博弈研究如何公平地重新分配用水收益。Kahil等 [5]将合作博弈运用在解决干旱和半干旱流域的水资源共享问题。Xiao等 [6]将水资源需求管理计划纳入CWAM,研究在此情况下如何分享收益。上述研究都是在确定的条件下提出水资源配置方案,但实际上水资源配置会受到诸多不确定因素的影响 [7]。各地区更愿意以不同的参与度同时参与到多个合作联盟。于是学者们纷纷转向运用模糊联盟合作博弈来解决不确定性条件下的水资源配置问题。Sadegh等 [8,9]建立模糊合作联盟,分别运用模糊Shapley、模糊最小核和模糊弱最小核等方法进行水资源分配,研究表明参加模糊合作联盟可以获得较清晰合作联盟和不参加联盟更高的收益。Abed-Elmdoust等 [10]针对流域间和流域内水量分配问题建立模糊合作博弈,结果表明该方法适用于解决现实世界中不确定的流域水资源分配的公平和效率问题。近年来,学者们开始探讨运用模糊联盟合作博弈解决水资源的优化配置问题。孙冬营等 [11]提出利用“优先原则”将初始配置的水资源通过构建模糊合作联盟进行二次优化配置。He等 [12]运用模糊联盟合作博弈确定利益相关者的初始水资源份额,并完成水资源和净效益的重新分配。谭佳音等 [13,14]先后针对群链产业合作模式和水资源短缺区域分别探讨水资源二次优化配置。这些研究得出:运用模糊联盟合作博弈解决水资源优化配置是有效和适宜的 [11,12],加入联盟不仅能够提升区域整体用水收益,各地也可以获得比单独利用水资源更高的收益 [13,14]。但同时从以上研究也发现,模糊联盟合作博弈虽然可以解决合作中存在的模糊性,但却无法反映参与者加入联盟的犹豫度。在流域水资源跨区域配置合作中,有意愿参与合作的地区并不是很确定地以既定的参与率参与合作,参与时往往会有很多考虑,表现为犹豫与等待。因此,各地区的参与程度不应该像已有研究在分析中设定为一个确定的数值,而应该是一个区间值,这就属于比较复杂的直觉模糊联盟合作博弈问题。
基于以上分析,本文在研究方法上首次提出运用直觉模糊联盟合作博弈解决跨区域水资源优化配置问题,允许参与合作的地区存在犹豫加入直觉模糊合作联盟;在研究对象上,本文选取长江、黄河、淮河和海河等主要流域作为研究对象,这些流域相互间存在跨区域调水,用真实数据可以更好检验方法的合理性与有效性,弥补现有研究侧重于纯理论分析的不足;在配置原则上,选择用水收益率高低作为“水资源优先配置原则”,优先将水资源分配给收益率高的地区,分配依据比较直观和高效。本文首先遵照水资源二次配置“优先原则”,以清晰联盟合作的水资源优化配置模型为基础,构建基于模糊联盟合作博弈的水资源优化配置模型和合作收益函数,提出运用基于Choquet积分的模糊Shapley值计算最优解;然后基于以上两个模型构建基于直觉模糊联盟合作博弈的水资源优化配置模型和合作收益函数,提出运用直觉模糊集、连续有序加权平均算子等构建具有区间Choquet积分形式的直觉模糊Shapley值求解最优解;最后对三种合作模型计算的我国主要流域水资源二次配置结果进行对比分析。研究结果将为我国主要流域实际开展跨区域水资源优化配置合作提供科学决策依据。
1 流域水资源优化配置方法水资源初始配置主要是确保本区域用水主体基本的生活生产用水需要。初始配置后,水资源丰富地区仍有水资源未得到充分利用,水资源短缺地区的用水需求也未得到有效满足,这都需要通过建立合作联盟开展水资源二次配置。二次分配按照“优先原则”,首先把水资源分配给联盟内用水收益率最高的地区,满足其需求后再把水资源分配给用水收益率次高的地区,以此类推,直到富余的水资源分配完为止 [11,14]。
1.1 基于清晰联盟合作博弈的水资源优化配置模型各地区的目标都是追求期望利益最大化,选择加入能给自己带来最大效益的联盟。各地区要么参与合作,要么不参与合作。参与合作的地区形成的联盟称为清晰联盟。所有地区参与合作就会形成大联盟,记为N={1,2,⋯,n},i表示第i个地区,i=1,2,⋯,n。
假定1:所有地区组成的具有清晰联盟且有实值支付的合作博弈用向量组(N,V)表示。部分地区组成的清晰联盟记为S,S是N的子集。
假定2:地区i在水资源初始配置时可获得的配额为Xi,单独利用水资源的用水收益率为bi(按降序排列为b1≥b2≥b3≥⋯≥bn),单独利用水资源的需求量上限为Ci。
假定3:清晰联盟S拥有的水资源总量AS是初始配置中所有地区获得的水资源初始配额之和,表示为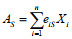
清晰联盟S的合作收益函数V(S)是将每个地区二次分配得到的水资源量乘以用水收益率后加总而得,可以表示为 [14]:
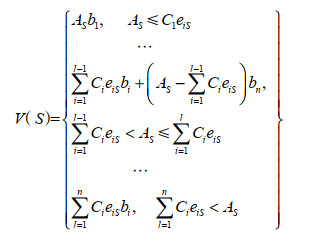
|
(1) |
清晰联盟合作收益的分配可以用Shapley值进行求解。
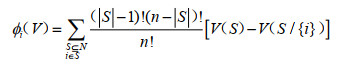
|
(2) |
其中,|S|表示清晰联盟S中的地区个数;(|S|-1)!(n - |S|)!/n! 表示地区i参与清晰联盟S的概率;V(s)与V(s/{i})的差值表示地区i对清晰联盟S所做的边际贡献。清晰联盟合作博弈(N,V)满足有效性、对称性、可加性和哑元性,Shapley值存在且唯一 [15]。
1.2 基于模糊联盟合作博弈的水资源优化配置模型由于受资源禀赋、自身能力、风险分摊等因素的影响,各地区更愿意开展多方合作。本文引入模糊集的隶属度(即参与度),构建基于模糊联盟合作博弈的水资源优化配置模型。只有当所有地区对联盟的参与度为0或1时,模糊联盟才退化为清晰联盟。
假设1:所有地区组成的具有模糊联盟且有实值支付的合作博弈用向量组(N,σ)表示,部分地区组成的模糊联盟记为S。
假设2:地区i在模糊联盟S的参与度为µS(i)∈[0, 1],用地区i提供的水资源量与初始配置获得的水资源量的比值表示。模糊联盟S中地区i的参与度集合可以表示为{ < i,µS(i)>}(i∈S)。
假设3:地区i在模糊联盟S中的水资源需求量上限为Di,它与地区i在模糊联盟S的参与度µS(i)以及在清晰联盟S的需求量上限Ci有关,表示为 [14] Di= µS(i)Ci。
假设4:模糊联盟S拥有的水资源总量AS表示为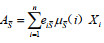
假设5:令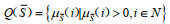
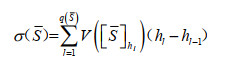
|
(3) |
其中,l=1,2,⋯,q(S);h0=0;[S]hl = {i|µS ≥ hl, i∈N} 表示模糊联盟S中参与度不低于hl的地区集合。
模糊联盟S的合作收益函数σ(S)可以表示为:
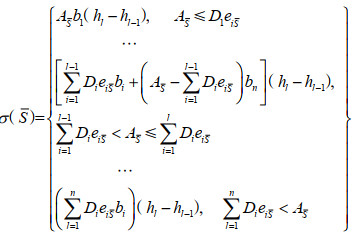
|
(4) |
基于Choquet积分的模糊联盟合作博弈(N,σ)的Shapley值是满足整体有效性、对称性、可加性和哑元性的唯一值 [17],表示为:
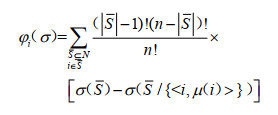
|
(5) |
愿意参与合作的地区在现实中往往不确定以既定的参与率参与合作,这使得各地区的参与度不是一个确定的数值,而是一个区间值。引入直觉模糊集的隶属度(参与度)、非隶属度(非参与度)和犹豫度,构建基于直觉模糊联盟合作博弈的水资源优化配置模型。只有当所有地区对联盟的犹豫度都为0时,直觉模糊联盟才退化为模糊联盟。
假设1:所有地区组成的具有直觉模糊联盟且有实值支付的合作博弈用向量组(N,γ)表示,部分地区组成的直觉模糊联盟记为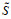
假设2:地区i在直觉模糊联盟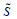
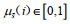
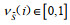
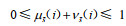
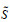
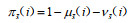
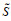
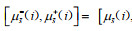
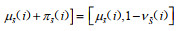
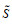
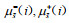
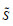
假设3:令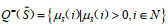
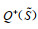
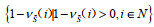
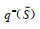
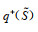
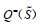
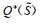
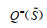
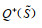
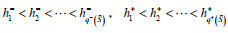
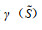
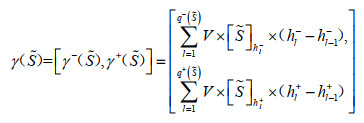
|
(6) |
其中,l=1,2,⋯,q(S);h0−=h0+=0;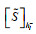
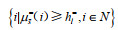
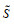
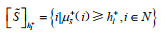
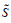
假设4:如果函数P(x):[0, 1] → [0, 1],为基本单位区间单调增函数(BUM),满足P(0)=0,P(1)=1,设[m,n] 为区间数,则有:
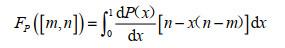
|
(7) |
称FP为连续有序加权平均(COWA)算子 [19,20]。P(x)函数的确定与各地区的决策偏好有关,称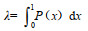
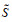
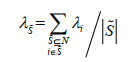
|
(8) |
假设5:利用态度因子将直觉模糊联盟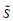
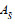
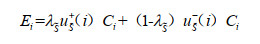
|
(9) |
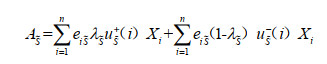
|
(10) |
假设6:利用态度因子将具有区间值的合作收益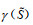
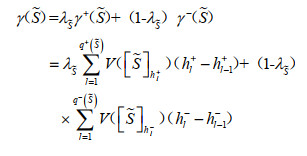
|
(11) |
因此,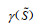

|
(12) |
具有区间Choquet积分形式的直觉模糊联盟合作博弈(N,γ)的Shapley值是满足整体有效性、对称性、可加性和哑元性的唯一值 [15],可以表示为:
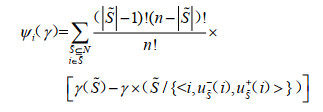
|
(13) |
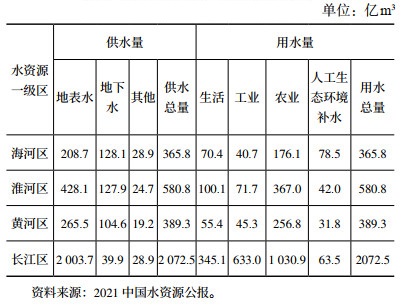
我国水资源区划主要采取三级体系,水资源一级区覆盖了我国的主要流域。现有水资源一级区10个,其中北方地区6个,南方地区4个。水资源一级区水资源量如表 1所示。2021年一级区水资源总量为29 638.2亿m3,其中地表水资源量为28 310.5亿m3,占水资源总量的95.5%;北方6区地表水资源量为6273.1亿m3,南方4区地表水资源量为22 037.4亿m3,分别占全国(不包括港澳台地区)地表水资源量的22% 和78%。南北地区水资源量差距大,南方地区水资源量较为丰富,北方地区水资源量较为缺乏。
| 表 1 2021年水资源一级区水资源量 |
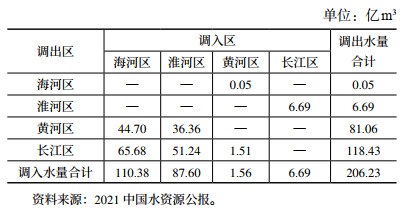
本文选取海河、淮河、黄河和长江等主要流域的水资源一级区作为研究对象,分别设为地区1、2、3、4;选取地表水资源量作为主要水资源量指标,地区之间发生跨流域调水就认定为形成合作联盟,于是存在联盟{1, 3}{1, 4}{2, 3}{2, 4}{3, 4}{1, 3, 4}{2, 3, 4} {1, 2, 3, 4}。四区域供水量和用水量见表 2,跨流域调水量见表 3。
| 表 2 2021年四区域供水量和用水量 |
| 表 3 2021年四区域跨流域调水量 |
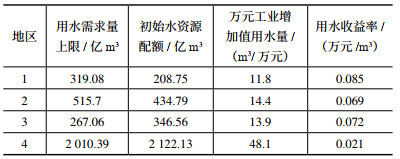
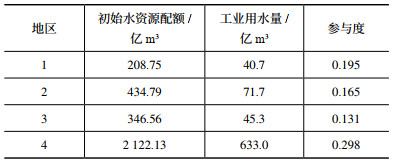
假定地区i提供的水资源量和从其他区调入的水资源量之和作为地区i的水资源需求量上限Ci;地区i提供的水资源量和从本地区调出的水资源量之和作为地区i拥有的初始水资源配额Xi;地区i愿意将初始获得的水资源全部投入清晰联盟合作中,且主要用于满足工业用水需要;地区i的用水收益率采用工业部门用水收益率,由各地区万元工业增加值用水量换算求得 [14]。主要参数如表 4所示。
| 表 4 清晰联盟各地区主要参数 |
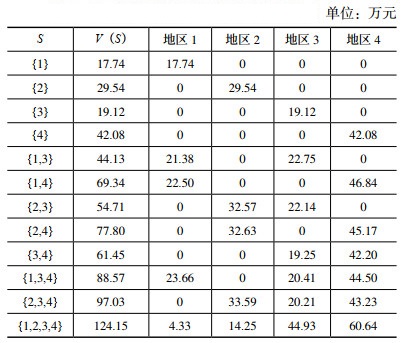
根据表 3和表 4提供的基础数据,代入式(1)和(2),可以计算得到不同清晰联盟组合下的合作收益V(S)及各地区在联盟中分配到的收益,如表 5所示。
| 表 5 不同清晰联盟组合下的收益分配结果 |
分析表 5的数据发现,在不同清晰联盟下,每个组合的合作收益都等于各地区分得的收益之和,说明满足有效性,符合集体理性;除大联盟{1,2,3,4} 外,其余组合中各地区的收益都大于不合作时的个体收益,说明满足可加性,符合个体理性。因此,对除大联盟外的所有清晰联盟合作是存在且有效的。具体来看,海河区(地区1)若不参与任何联盟,仅通过初始配置水资源可获得收益17.74万元;与黄河区(地区3)合作进行水资源二次配置可分得收益21.38万元,与长江区(地区4)合作可分得收益22.50万元;与黄河区和长江区形成三区联盟可分得收益23.66万元,高于两两联盟的收益;与淮河区、黄河区和长江区形成大联盟仅能获得收益4.33万元。淮河区(地区2)有完全类似的情况,即三区联盟获得的收益高于两两联盟,两两联盟获得的收益高于不参与联盟,不参与联盟获得的收益高于四区联盟。黄河区(地区3)和长江区(地区4)情况稍有不同,虽然参与两两联盟后两地区获得的收益都高于不合作时,但参与三区联盟获得的收益不一定好于两两联盟;当形成全联盟时,黄河区和长江区却可以获得远高于其他情况的收益。分析原因发现,海河区和淮河区的初始水资源配额无法满足地区发展对水资源的需求,黄河区和长江区相比而言初始水资源仍有部分富余。对于水资源有需求缺口的海河区和淮河区而言,肯定愿意与黄河区、长江区开展水资源二次配置合作,但是并不需要四区形成合作联盟,因为海河区和淮河区都属于需水方,两地区之间合作意义不大。黄河区和长江区作为水资源输出方,需要更多地与水资源有需求的海河区和淮河区合作更好,两区之间的水资源调配实现价值相对较低。鉴于不同水资源一级区的情况,为了让合作各方都取得较满意的收益,水资源二次配置合作仍应该选择以部分地区形成合作联盟更为可行。
2.3.2 基于模糊联盟合作博弈的水资源优化配置模型计算结果假定地区i没有把获得的初始水资源配额全部投入到合作联盟,而是提供一部分去满足联盟需要的工业用水;将地区i的工业用水量与计算获得的初始水资源配额之比作为地区i的联盟参与度。主要参数如表 6所示。
| 表 6 模糊联盟各地区主要参数 |
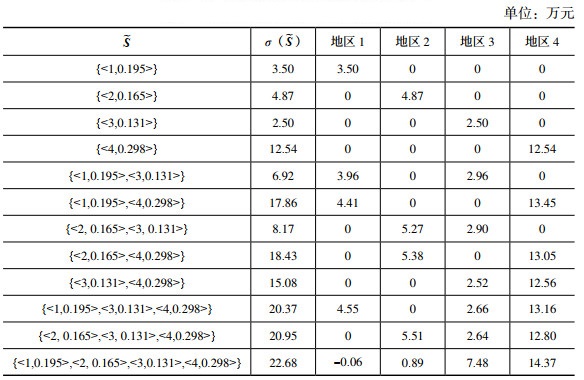
根据表 6提供的基础数据,代入式(4)和式(5),可以计算得到不同模糊联盟组合下的合作收益σ(S)及各地区在联盟中分配到的收益,如表 7所示。
| 表 7 不同模糊联盟组合下的收益分配结果 |
从表 7数据看出,在模糊联盟组合下,除大联盟{1, 2, 3, 4} 外,每个组合的合作收益都等于各成员分得的收益之和,同时组合中各成员获得的收益都大于不合作时的个体收益,说明符合集体理性和个体理性。这表明对除大联盟{1, 2, 3, 4} 外的所有模糊联盟合作是存在且有效的。模糊联盟中各地区以一定的参与率参与联盟,获得的收益都低于清晰联盟,这是正常的。对于海河区(地区1)和淮河区(地区2)而言,参与三区联盟获得的收益高于两两联盟,参与两两联盟获得的收益高于不参与联盟,不参与联盟获得的收益高于参与四区联盟。四区联盟相对三区联盟增加的是需水方,会减少同样需水的海河区和淮河区获得的水资源量,所以两地区会因为参与大联盟出现用水收益大幅下降甚至亏损的局面。对于黄河区(地区3)和长江区(地区4)而言,参与三区联盟获得的收益不一定高于两两联盟获得的收益,但是两地区会在大联盟中实现高于两两联盟和三区联盟的收益。这是因为四区合作可以让水资源供给方与水资源有需求的海河区和淮河区同时展开合作,对于供给方而言是有利的。由此可见,模糊联盟与清晰联盟得到的结论完全相同。在模糊联盟条件下,水资源一级区合作仍应该以部分合作联盟为主,使得各方都获得相对较高的收益。
2.3.3 基于直觉模糊联盟合作博弈的水资源优化配置模型计算结果假定地区i参与联盟存在犹豫,二次配置时会考虑是优先满足联盟需要的工业用水还是本区域其他生活用水(初始配置已经保证本地区的生活和生态用水需要);将地区i可以提供的工业用水量与初始水资源配额之比作为地区i的参与度µS(i),同时将地区i可以提供的生活用水量与初始水资源配额之比作为地区i的非参与度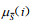
| 表 8 直觉模糊联盟各地区主要参数 |
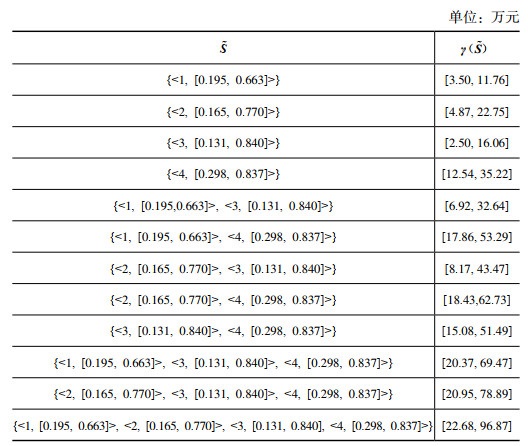
根据表 8提供的基础数据,代入式(6),可以计算得到不同直觉模糊联盟组合下的合作收益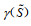
| 表 9 不同直觉模糊联盟组合下的联盟收益 |
使用COW算子将具有区间值的合作收益集结为实数。假设Q(y)= yr为基本单位区间单调增函数,根据各地区的参与度均值大小,地区1设为Q1(y)= y,地区2设为Q2(y)= y2,地区3设为Q3(y)= y3,地区4设为Q4(y)= y4。由此可以求得各地区的态度因子λ。
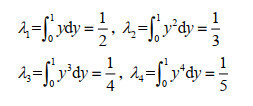
|
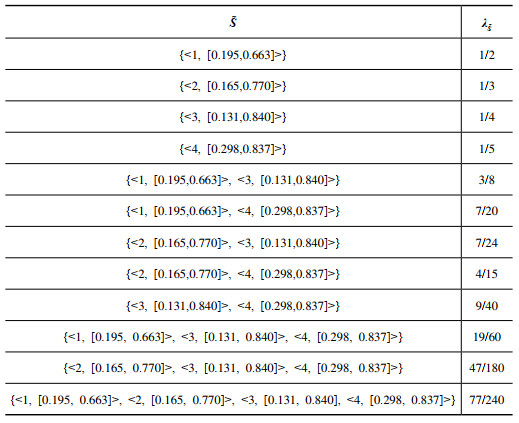
不同直觉模糊联盟的态度因子如表 10所示。
| 表 10 不同直觉模糊联盟的态度因子 |
根据表 10,运用式(9)和式(10)将水资源需求量上限Ei和拥有的水资源总量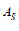
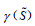
| 表 11 不同直觉模糊联盟组合下的集结收益和收益分配结果 |
在直觉模糊联盟组合下,除大联盟{1,2,3,4} 外,每个联盟组都同时满足集体理性和个体理性,说明对除大联盟{1,2,3,4} 外的所有直觉模糊联盟合作是有效且稳定的。分析表 10的数据可知,不论是组成两两联盟还是三者联盟,各地区的收益均好于不形成联盟时的收益。对于海河区(地区1)和淮河区(地区2)而言,参与三者联盟获得的收益都好于两两联盟,对于黄河区(地区3)和长江区(地区4)而言,参与三者联盟获得的收益不一定好于两两联盟。四地区形成大联盟后,对于海河区和淮河区可获收益依然会大幅下降,黄河区和长江区依然会在大联盟中收益更多。将表 11与表 7对比,发现不论各地区是否参与合作,直觉模糊联盟获得的收益全部高于模糊联盟。这说明各地区参与联盟虽然存在犹豫,但只要尽量争取使得每个地区变犹豫为参与,将会获得相较于模糊联盟更高的收益。直觉模糊联盟与前面两种联盟得到的结论完全相同。在直觉模糊联盟条件下,依然不应盲目追求联盟越大越好,各方应根据自身实际情况有选择地参与部分合作联盟。
3 研究结论与启示我国是一个水资源消耗的大国,但并不是水资源利用的强国。为了更好地提高水资源综合利用的效率和效益,水资源初始配置后的二次配置是解决水资源地区供需矛盾、实现水资源可持续利用的必然选择。本文研究主要取得以下三方面的成果:
(1)首次提出运用直觉模糊联盟合作博弈解决水资源优化配置问题。在水资源跨区调配中,各地区参与合作需要考虑的因素很多,选择哪个联盟加入效益最大,以何种程度加入联盟更好,势必存在一定的犹豫度。运用清晰联盟合作博弈只能表示地区完全参与到一个特定的联盟,运用模糊联盟合作博弈只能表示地区以一定的参与度加入联盟,两种方法都无法准确反映地区参与合作的真实状态。构建基于直觉模糊联盟合作博弈的水资源优化配置模型,可以把参与地区的参与度、非参与度和犹豫度同时反映出来。运用直觉模糊集、连续有序加权平均算子等构建具有区间Choquet积分形式的直觉模糊Shapley,最终可以计算出合作收益的最优分配解。求解结果经证明是稳定且唯一的,说明该方法是可行的,可以使用该方法解决水资源优化配置问题。
(2)使用我国主要流域的真实数据验证方法的正确性。我国主要流域作为水资源一级区每年都有跨流域调水的需求,这充分说明各流域地区希望通过水资源调配实现水资源的优化配置。以我国主要流域的实际数据进行测算,较以往用数值算例验证的方式可以更好地检验方法的可操作性及有效性。本文在处理实际数据时注重解决两个关键问题:首先,如何处理用水公平与效率的关系。本文的解决方式是遵照水资源二次配置“优先原则”。考虑到各地区在发展经济中主要是工业用水导致的供需矛盾突出,选择将工业用水作为调配用水,利用各地区万元工业增加值用水量换算求得工业用水收益率,按照工业用水收益率高低作为“优先原则”对水资源进行配额调整。这种分配原则在实际运用中比较容易实现。其次,如何选择水资源跨区合作的对象,如何共享合作收益。本文的解决方式是分别构建基于清晰联盟合作博弈、模糊联盟合作博弈和直觉模糊联盟合作博弈模型的水资源优化配置模型及合作收益函数,通过Shapley值的求解,对比分析三种合作模式下各种联盟的合作收益及个体收益,找到最优的水资源优化配置模型以及最佳的地区合作模式。
(3)与已有研究成果的比较。第一,各地区参与水资源二次配置,无论构成的是清晰合作联盟、模糊合作联盟还是直觉模糊合作联盟,都取得相较于不合作更好的合作收益。已有研究并没有对三种情况做过全面对比,本文将三种联盟下的合作收益和个体收益进行比较,更能有助于比较方法的优劣以及选择最佳的合作模式。第二,各地区参与直觉模糊合作联盟获得的收益全部高于参与模糊合作联盟获得的收益,这说明各地区面对参与联盟的犹豫,只要尽量争取使每个地区变犹豫为参与,将会获得相较于模糊联盟更高的收益。已有研究并没有采用直觉模糊合作博弈研究此类问题,本研究可以证明直觉模糊联盟合作博弈是可行且更合适的研究方法。第三,在直觉模糊合作联盟中,水资源需求方只希望与水资源供给方更多地开展合作,所以联盟规模并不一定越大收益越多,尤其是增加的联盟成员同样属于需求方,这样的大联盟还不如部分联盟,正如本文研究中的海河区和淮河区;水资源供给方希望把富余的水资源满足更多水资源需求方的要求,所以对他们而言联盟规模是越大收益越多,正如本文研究中的黄河区和长江区。因此,为了实现合作各方的共赢,不应盲目追求联盟的规模,应根据地区自身实际情况,有选择地参与合作联盟。已有研究没有使用直觉模糊联盟合作博弈方法,所以就无法得到以上结论。
综上,本文运用直觉模糊联盟合作博弈方法构建水资源优化配置模型,对解决我国主要流域的水资源优化配置问题提供了一种新的解决思路。水资源一级区在初始配置保证本地区基本用水的前提下,可以根据自身实际参与到水资源二次配置合作中。本方法的运用可以帮助我国主要流域地区选择最佳的合作对象,合理地分配合作收益,既能提高水资源综合利用效率,又能获取一定的合作收益,实现多方共赢的合作成效。
| [1] |
王泽琳, 张如良, 吴欢. 跨流域调水的公正问题——基于环境正义的分析视角[J]. 中国环境管理, 2019, 11(2): 101-105. |
| [2] |
孙冬营, 余梦玲, 马剑锋, 等. 供需变化情景下破产理论在流域水资源配置中的应用[J]. 长江科学院院报, 2023, 40(9): 17-23, 31-31. |
| [3] |
WANG L Z, FANG L P, HIPEL K W. Water resources allocation: a cooperative game theoretic approach[J]. Journal of environmental informatics, 2003, 2(2): 11-22. DOI:10.3808/jei.200300019 |
| [4] |
WANG L Z, FANG L P, HIPEL K W. Basin-wide cooperative water resources allocation[J]. European journal of operational research, 2008, 190(3): 798-817. DOI:10.1016/j.ejor.2007.06.045 |
| [5] |
KAHIL M T, DINAR A, ALBIAC J. Cooperative water management and ecosystem protection under scarcity and drought in arid and semiarid regions[J]. Water resources and economics, 2016, 13: 60-74. DOI:10.1016/j.wre.2015.10.001 |
| [6] |
XIAO Y, HIPEL K W, FANG L P. Incorporating water demand management into a cooperative water allocation framework[J]. Water resources management, 2016, 30(9): 2997-3012. DOI:10.1007/s11269-016-1322-x |
| [7] |
涂燕, 石宏伟, 秦晋栋, 等. 混合不确定环境下双层多目标区域水资源优化配置研究[J]. 系统工程理论与实践, 2023, 43(8): 2428-2446. |
| [8] |
SADEGH M, MAHJOURI N, KERACHIAN R. Optimal inter-basin water allocation using crisp and fuzzy Shapley games[J]. Water resources management, 2010, 24(10): 2291-2310. DOI:10.1007/s11269-009-9552-9 |
| [9] |
SADEGH M, KERACHIAN R. Water resources allocation using solution concepts of fuzzy cooperative games: fuzzy least core and fuzzy weak least core[J]. Water resources management, 2011, 25(10): 2543-2573. DOI:10.1007/s11269-011-9826-x |
| [10] |
ABED-ELMDOUST A, KERACHIAN R. Water resources allocation using a cooperative game with fuzzy payoffs and fuzzy coalitions[J]. Water resources management, 2012, 26(13): 3961-3976. DOI:10.1007/s11269-012-0115-0 |
| [11] |
孙冬营, 王慧敏, 于晶. 基于模糊联盟合作博弈的流域水资源优化配置研究[J]. 中国人口· 资源与环境, 2014, 24(12): 153-158. |
| [12] |
HE Y H, YANG J, CHEN X H. Allocating river water in a cooperative way: a case study of the Dongjiang River Basin, South China[J]. Stochastic environmental research and risk assessment, 2018, 32(11): 3083-3097. DOI:10.1007/s00477-018-1526-0 |
| [13] |
谭佳音, 蒋大奎. 群链产业合作模式下"京津冀"区域水资源优化配置研究[J]. 中国人口· 资源与环境, 2017, 27(4): 160-166. |
| [14] |
谭佳音, 蒋大奎. 基于水资源合作的水资源短缺区域水资源优化配置[J]. 系统管理学报, 2020, 29(2): 377-388. |
| [15] |
南江霞, 关晶, 王盼盼. 基于Choquet积分的直觉模糊联盟合作博弈的Shapley值[J]. 运筹与管理, 2019, 28(9): 41-46. |
| [16] |
韩婷. 具有直觉模糊联盟的合作企业利益博弈分配方法研究[D]. 福州: 福州大学, 2014.
|
| [17] |
杨靛青, 李登峰. 模糊合作博弈方法及应用[M]. 北京: 科学出版社, 2021.
|
| [18] |
孙红霞. 基于Choquet积分形式的模糊联盟核心[J]. 运筹与管理, 2015, 24(1): 93-99. |
| [19] |
卢琇珺, 吴和成. 连续区间数的中位算子及其灵敏度分析[J]. 运筹与管理, 2017, 26(7): 164-169. |
| [20] |
周代娣, 陈华友, 张倩昀, 等. 基于COWA算子的相关性区间组合预测优化模型及其近似求解[J]. 中国科学技术大学学报, 2020, 50(5): 673-681. |
 2024, Vol. 16
2024, Vol. 16