2. 环境前沿技术北京实验室, 北京 100084;
3. 中国地质大学(武汉)经济管理学院, 湖北武汉 430074
2. Beijing Laboratory of Environmental Frontier Technologies, Tsinghua University, Beijing 100084, China;
3. School of Economics and Management, China University of Geosciences, Wuhan 430074, China
2020年9月22日,中国在第七十五届联合国大会一般性辩论上宣布了“努力争取2060年前实现碳中和”的目标。2021年3月,在《第十四个五年规划和二〇三五年远景目标纲要》中,中国政府再次强调“落实2030年应对气候变化国家自主贡献目标”和“锚定努力争取2060年前实现碳中和”。在低碳转型过程中,碳强度是关键的约束性指标,这一指标不仅反映了碳排放,还体现了经济增长与环境之间的协调关系[1]。2009年的哥本哈根世界气候会议上,中国首次提出了2020年单位国内生产总值(GDP)的二氧化碳排放量较2005年下降40 %~50 % 的碳强度目标[2]。在“十四五”规划中,中国又一次明确指出在低碳转型过程中必须要实施“以碳强度控制为主”的制度。因此,探求影响碳强度的关键因素对低碳政策制定具有重要意义。电气化对决定碳强度的两个因素(碳排放和经济增长)都具有重要的影响。一方面,终端能源消费的电气化能够直接影响CO2排放;另一方面,电力消费与经济增长之间存在因果关系。中国的电气化进程已经取得了巨大进步。在工业化和城市化过程中,中国的电气化得到了快速的发展,电气化水平从1997年的14 % 大幅度上升到2016年的22 %,基本与美国(22 %)和欧盟(23 %)等发达国家处于同一水平[3]。同时,我国终端能源消费的电气化仍然保持着增长势头,2016年国家发展改革委等八部门联合印发《关于推进电能替代的指导意见》以完善电能替代配套政策体系,推进电能替代趋势。
在碳中和的背景下,国际能源署(International Energy Agency,IEA)等机构预测,中国2050年的终端电气化程度将达到50 % 甚至更高[4, 5]。但是在目前的研究当中,电气化和碳强度之间的关系特征尚不明朗。基于此背景,本文以中国30个省份(因数据所限,未包括西藏及港澳台地区)为样本,综合考虑了影响碳排放强度的多种因素,通过面板模型及空间计量模型实证检验了电气化与碳排放强度之间存在的倒U形关系,为电气化政策制定提供了参考。
1 文献综述与理论假设终端能源消费的电气化在理论上通常被认为是降低碳排放的有效手段[6, 7]。2018年,中国工业、交通和住宅与商业部门的CO2排放量占总排放量的43.4 %[3],通过电力工业装备、电动汽车、电热设备和电用炊具等电气化设施进行电能替代可以在这些部门带来显著的直接减排效益[8-11]。但与此同时,电气化过程也存在着排放风险。Peng等人的研究指出,如果保持目前电力生产的能源结构,电气化水平的提高可能会带来额外的排放[12]。Hofmann等人使用环境扩展的投入产出模型对交通部门的电气化进行研究,发现只有在使用煤电比例低于50 % 的电力时,电动汽车的大规模推广才会实现显著的减排效益[8]。与电气化和排放的关系不同,主流研究普遍认为其对经济增长具有显著的正面影响[13, 14]。但是,电力消费对经济发展的促进作用也存在异质性。在时间上,周绍杰等人基于增长回归模型, 得到了电力消费对促进经济增长的长期影响明显高于短期影响的结论[14]。在空间上,李强等人指出电气化对东部地区经济增长的促进效果优于西部地区[15]。在规模上,王绵斌等人发现电力投资对促进经济发展存在门槛效应,不同规模的电力投资对京津冀和长三角地区经济的促进效果存在差异[16]。在类型上,齐绍洲和李杨通过面板向量自回归验证了可再生电力对经济增长的额外促进效果[17]。王帅也建立向量自回归模型证明了清洁能源的使用促进了中国经济的可持续发展[18]。
基于上述文献分析,本文认为电气化和碳强度之间可能存在非线性关系。一方面,电气化与碳排放之间的关系仍然存在争议,另一方面,虽然电气化对经济的促进作用得到认可,但是其影响效果在不同层面存在异质性。根据当前的研究,首先,随着可再生电力对电气化的贡献逐渐增大,电气化增长可能带来更有效的减排和额外的经济促进效果。其次,电气化的发展可能也存在规模效应,当其达到一定水平时会对生产效率和产业结构带来更显著的影响,同时促进排放降低和经济发展。再者,电气化长期影响效果的发挥和区域间经济差异缩小带来的电气化收益提高也可能起到进一步降低碳强度的作用。因此,我们认为电气化和碳强度之前可能存着倒U形的环境库兹涅茨曲线(EKC)关系。
林伯强和蒋竺均首次进行了中国CO2排放拐点的预测,此后有众多学者对不同因素与CO2间的EKC关系进行了检验[19]。但是在EKC实证研究中,研究者通常根据地理区域或行政区划的截面数据和面板数据进行计量分析。这种分析思路是基于区域间的污染排放和环境恶化互不关联的前提,然而这与实际情况并不符合。首先,工业布局、能源消费结构和污染治理投资能力等在空间上都存在显著的聚集,这使得电气化、CO2排放和经济发展在客观上存在空间相关性。其次,区域间的贸易对双方的经济和环境都产生了影响[20],高电气化地区由于其高效的生产方式可能吸引了更多的投资与生产。再者,我国区域发展也并不平衡,东中西部地区的经济发展路径和经济发展特征具有显著差异,这在实际上形成了区域间的“俱乐部收敛” [21]。因此,如果主观上回避空间相关性影响的存在,对EKC模式是否存在的估计可能是有偏差的,相应的参数检验结果也可能是不合理的。朱平辉等人认为对空间要素的忽略可能是部分EKC研究中参数估计不够稳健或不同研究中结论相互矛盾的重要原因之一[22]。因此,在涵盖了空间尺度的EKC研究中,引入空间计量分析是合理的。
目前,已经有许多文献采用空间计量模型对EKC进行研究。郝宇等关注了空间效应对EKC曲线拐点的影响,其使用空间杜宾模型(Spatial Durbin Model,SDM)研究了中国能源消费和电力消费的EKC,并发现空间因素可能会导致拐点后移[23]。Ding等利用空间计量模型证明了北京-天津-河北地区的经济增长与PM2.5浓度存在EKC关系,并同样发现了考虑空间效应后会使拐点推迟的现象[24]。
基于上述文献,本文先验地认为碳强度可能随着电气化水平的提高先上升后下降,相应地,本文关注了EKC在空间上的稳健性。据此,我们提出以下两个假设:
H1:中国电气化水平与碳强度之间存在EKC关系。
H2:电气化与碳强度的EKC关系在考虑了空间因素后依然存在。
2 模型方法及数据 2.1 EKC的方程形式可拓展的随机性的环境影响评估模型(Stachastic Impacts by Regression on Population, Affluence, and Technology,STIRPAT)作为分析经济与环境关系的工具被广泛应用于检验经济增长与环境污染之间的EKC关系[25]。本文使用了扩展的STIRPAT模型:
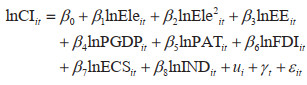
|
(1) |
式中,i和t分别表示省份和时间;CI是被解释变量,表示碳强度,由单位GDP(2010年不变价格)的二氧化碳排放量表示;Ele表示电气化水平,即电力消费占终端能源消费比重;EE表示能源效率;PGDP表示人均GDP(2010年不变价格);PAT表示发明专利数量;FDI表示境外直接投资额;ECS表示能源消费结构;IND表示产业结构。β1和β2是解释变量的系数;β3~β8为控制变量的系数。β0表示常数项;ui表示个体效应;γt表示时间效应;εit表示随机误差项。控制变量指标选择的依据如下:
(1) 能源效率。能源效率的提高是促进经济高质量发展和减少CO2排放的重要途径。本文采用各省份能源消费总量与GDP(2010年不变价格)的比值进行表示(2010年不变价格)。
(2) 人均GDP。用于表示地区总体经济发展情况。
(3) 发明专利数量。反应地区技术水平,先进的生产技术是碳强度下降的重要驱动因素。
(4) 境外直接投资额。境外投资既可能带来低碳技术和先进的环境管理手段,促进国内进行产业升级,降低碳强度,也可能带来“污染天堂”,对碳强度有重要影响。
(5) 能源消费结构。能源消费结构通常被认为是影响碳强度的重要原因,本文用各省份煤炭消费与总能源消费之比进行表示。
(6) 产业结构。第二产业的化石能源燃烧是排放的主要来源之一,此外第二产业的投资回报率在三大产业中排名第一,对经济发展有重要影响[26]。本文采用第二产业增加值在GDP中所占比重来进行表示。
2.2 EKC空间计量模型空间计量模型是一种改进的面板计量模型,在空间相关性的讨论中被广泛应用。Anselin第一次在面板模型的基础上引入了空间滞后项和空间滞后误差项,将空间相关性引入到计量经济学中[27]。空间滞后模型(Spatial Lag Model,SLM)可以用来检验碳排放强度的空间依赖性,模型中包含一个被解释变量的空间滞后项。空间误差模型(Spatial Error Model,SEM)则是将误差项纳入了空间自回归中[27, 28]。实际应用中更具有解释意义的空间杜宾模型(SDM)由LeSage和Pace提出,模型中同时包含了被解释变量、解释变量以及控制变量的空间滞后项,可以帮助理解不同变量的空间溢出效果[29]。
根据空间相关性的不同引入形式[30],非空间计量模型式(1),可以具体拓展为以下三种模型。
2.2.1 空间滞后模型(SLM)
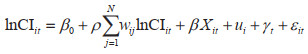
|
(2) |

|
(3) |
式中,ρ为空间自回归系数,表示碳排放强度的空间依赖性;wij是空间权重矩阵W的第i行和j列的元素,用于表示i省份和j省份的空间关系。空间矩阵既可以基于连续性进行设定也可以按照距离进行设定。本文采用基于连续性的空间权重矩阵,将具有公共边界的单元视为相邻区域,其设置规则如式(3)所示。为方便展示,此处用Xit代替表示式(1)等号右侧的解释变量和控制变量,β则为这些变量的系数。其他符号的含义与前文相同。
2.2.2 空间误差模型(SEM)
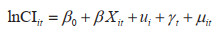
|
(4) |
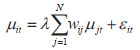
|
(5) |
式中,µit表示空间误差项;λ为空间误差系数,表示误差的空间依赖性;其他符号的含义与前文相同。
2.2.3 空间杜宾模型(SDM)
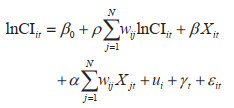
|
(6) |
式中,α表示空间滞后解释变量的系数;其他符号的含义与前文相同。
2.3 数据来源本文数据覆盖了1997-2016年中国30个省份(除西藏与港澳台地区)。省级层面电气化数据来自《中国能源统计年鉴》。地方人口数据、GDP、GDP平减指数、第二产业GDP增加值的数据来源均为《中国统计年鉴》。地方煤炭消费数量来自《中国能源统计年鉴》。发明专利数量出自《中国科技统计年鉴》。境外直接投资额来自Wind金融数据库。
目前,中国还没有官方公布的二氧化碳排放数据,因此本文首先需要对二氧化碳排放量进行计算。政府间气候变化专门委员会(IPCC)提出的排放因子法是目前进行碳排放量计算的主流方法,计算公式写作:
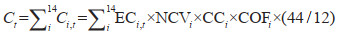
|
(7) |
其中,Ct表示t时期内的二氧化碳排放量;i表示各种能源燃料,包括煤炭、原油和天然气等14种化石燃料;Ci, t, 表示能源燃料i在时间t的排放量;ECi, t, 表示能源燃料i在时间t内的消耗量;NCVi表示能源燃料i的平均低位发热量;CCi表示能源燃料i的碳含量;COFi表示能源燃料i的碳氧化因子。44和12则分别为二氧化碳和碳的分子量[31]。30个省份在1997-2016年所有的能源消耗数据和平均低位发热量均来自1997-2016年《中国能源统计年鉴》中的能源均衡表。各化石燃料的碳含量和二氧化碳排放因子来自IPCC。
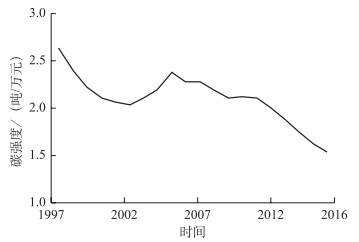
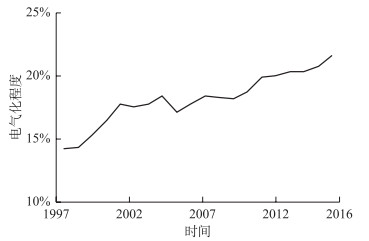
3 实证分析 3.1 碳强度与电气化现状图 1和图 2分别展示了中国1997-2016年的碳强度和电气化趋势。中国的碳排放强度整体处于下降趋势,中国2016年的碳排放强度为1.5吨/万元,较1997年下降了41.4 %。2002-2007年,碳排放强度出现反弹,从2.0吨/万元上升到2.3吨/万元。这主要是中国在2001年加入世界贸易组织后迅速承接了大量来自国际市场的碳密集型产业而导致的。中国的电气化水平则表现出稳定上升的趋势,从1997年的14.3 % 迅速提高到2016年的21.7 %。
|
图 1 中国1997-2016年的碳强度趋势 |
|
图 2 中国1997-2016年的电气化水平趋势 |
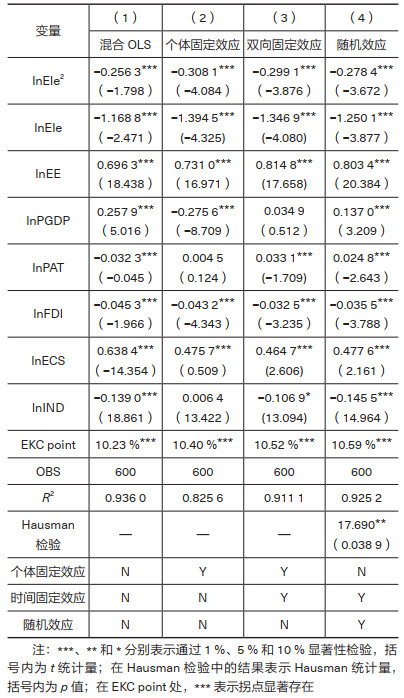
表 1给出了混合OLS模型(1)、固定效应模型(2)、双向固定效应模型(3)和时间固定随机效应模型(4)的估计结果。实证结果显示,无论采用何种模型进行检验,电气化水平与碳排放强度之间均存在显著的倒U形曲线,即lnEle2和lnEle的系数均显著为负。根据Hausman检验,我们选择固定效应模型而非随机效应模型,其中,双向固定效应模型的拟合效果好于个体固定效应。因此,本文以双向固定效应模型(3)的估计结果为准进行讨论。由双向固定效应模型的回归结果可知,EKC曲线拐点约在电气化为10.52 % 处,各模型回归结果估计的拐点范围在10.23 %~10.59 % 波动,说明10.52 % 的拐点估计结果较为稳健。截至2016年,所有省份的电气化水平都超过了10.52 % 的拐点,即使电气化水平最低的黑龙江省也达到了13.53 %。这意味着继续推进电气化发展,将稳健地发挥降低碳排放强度的作用,为我国电能替代政策的设计和执行提供了依据。
| 表 1 未考虑空间因素的电气化与碳强度的EKC关系检验 |
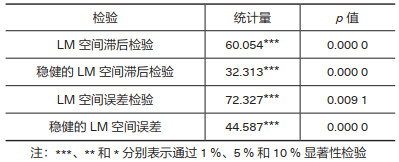
本文使用LM空间滞后(LM lag)、稳健的LM空间滞后(Robust LM lag)、LM空间误差(LM error) 和稳健的LM空间误差(Robust LM error)四种检验来识别选择何种空间计量模型[23]。表 2分别给出了以上检验的结果。结果显示LM lag、Robust LM lag、LM error和Robust LM error检验的所有统计量p值都小于0.01,即拒绝SDM模型可以退化为SLM模型和SEM模型的假设,因此初步判断SDM模型是合适的空间计量模型。
| 表 2 空间计量模型的选择与检验 |
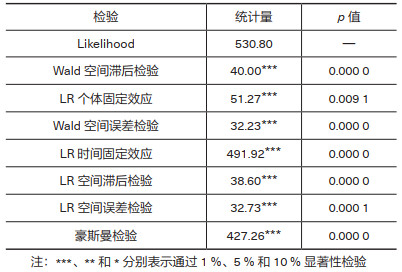
在通过LM检验初步确定SDM模型后,本文进一步对模型选择的稳健性和细分模型的选择进行检验[23]。表 3展示了对SDM模型进行进一步检验的结果。Wald检验和LR检验均表明,SDM模型简化为SLM或SEM模型的假设在1 % 显著性水平被拒绝,再次验证了选择SDM模型的合理性。Hausman检验则显著拒绝了随机效应模型,因此本文需要进一步对固定效应的具体形式进行选择。表 3展示了个体固定效应、时间固定效应和双向固定效应的LR检验结果,结果显示,个体固定效应的LR统计量为51.27,时间固定效应的LR统计量为491.92,在自由度为30(省份数目)和20(年份数)的情况下其对应的p值都小于0.01,因此两种固定效应不存在的原假设均被拒绝,本文最终选择使用双向固定的空间杜宾模型。
| 表 3 SDM模型稳健性和具体形式的选择与检验 |
通过表 2和表 3的检验可知,本文研究中纳入空间因素是合理且不可避免的,并且在空间计量模型中应当选择双向固定的SDM模型。一方面,理论上,SDM模型既包括碳排放强度的空间滞后也包括了解释变量的空间滞后,与SLM模型和SEM模型相比,在反映空间自相关性上更有优势,在空间计量模型中应该作为优先考虑的对象[23]。另一方面,本文实际检验中也已经证实,SDM模型不可以退化成SLM模型和SEM模型,并且个体与时间固定效应均被认为是必要的。
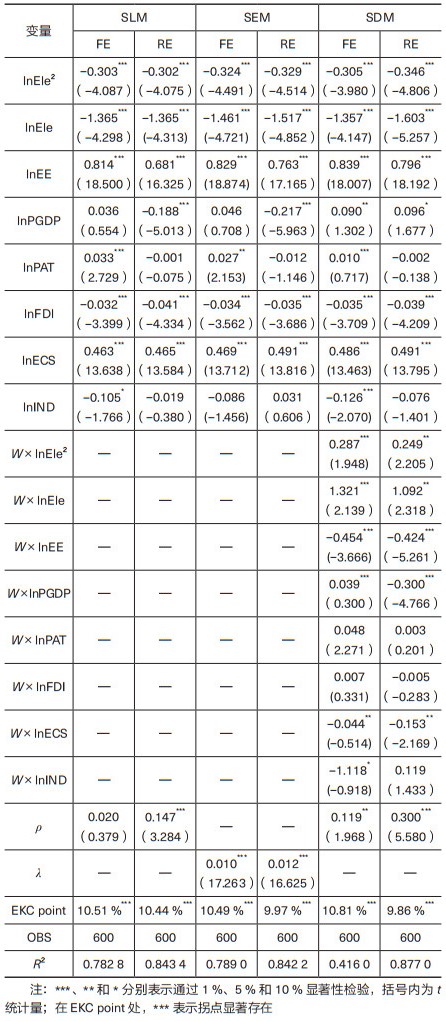
虽然已经证明SDM模型更适合本研究,本文依然对SLM模型和SEM模型的结果进行展示,以对分析起到辅助作用。如表 4所示,双向固定的SDM (FE)模型的回归结果显示,碳排放强度空间滞后ρ的估计系数显著为正,表明碳强度与空间因素存在显著的正相关性,即相邻地区的碳强度显著相关。在考虑了空间因素的影响后,六种模型中lnEle2和lnEle的系数仍然均显著为负。由估计出的系数可知,电气化与碳排放强度间的EKC关系在考虑空间因素后依然稳健,碳排放强度显著存在随着电气化提高先上升后下降的特征。所有模型的估计结果中,拐点的范围为9.86 %~10.81 %,这一结论与非空间模型的估计结果基本相似。以SDM(FE)模型结果为准,此时电气化与碳排放强度EKC的拐点位于电气化水平为10.81 % 处,较10.52 % 的拐点略有后移。自变量空间滞后项W×X (X指代本模型中各自变量)的回归系数反映了本地自变量变化对相邻地区碳强度造成的影响。W ×lnEle2和W ×lnEle的系数均显著为正,这表明当一个地区电气化水平上升的时候,它对相邻省份碳排放强度发挥的作用是使其先下降后上升。EKC拐点后移的原因可能与造成W ×ln EE和W ×ln IND的参数显著为负的原因相似,即一个区域的能源效率下降或第二产业比重上升可能会减少相邻地区的碳排放强度,而这种现象的产生是因为碳密集型产业的转移[32]。同理,相邻地区电气化水平提高后,更多高端产业转移到相邻地区,而碳密集型产业在本地比例则有可能相应提高。所以,在考虑了空间因素后,相邻省份电气化水平的上升可能会导致本地碳强度上升,因此本地电气化对碳强度倒U形曲线的拐点被后移了。
| 表 4 纳入空间因素的电气化与碳强度的EKC关系检验 |
虽然表 4中提供了SDM模型的回归结果,但是其系数不能像非空间计量模型一样完全反映变量对被解释变量的边际影响[23, 25],我们可以通过微分分解的方式将SDM(FE)的结果分解为直接效应、间接效应和总效应来解决这一问题。直接效应是指某一地区中自变量的变化对同一区域中因变量的影响,直接效应不仅考虑了本地区对本地区的影响,还考虑了本地区影响了其他地区后其他地区返还回来的影响,而间接效应是指某一区域中自变量对相邻区域因变量的影响,总效应就是直接效应与间接效应之和[28]。
表 5展示了双向固定效应SDM模型的直接、间接和总体效应。由于电气化间接效应的二次项和总效应都不显著,根据总效应计算的EKC拐点在统计意义上的可信度不高[23]。因此,直接效应中的转折点更为可靠,即电气化水平低于10.84 % 时,碳排放强度随电气化水平的提高而上升,超过10.84 % 后,碳排放强度随电气化水平的提高而下降。这一拐点的数值与SDM(FE)的结果近似,证明了结论的稳健性。而间接效应中lnEle系数显著为正,也印证了前文对于拐点右移的解释,即本地电气化水平的提高会显著增加相邻省份的碳强度。这一结果表明地区之间可能存在竞争效应,未来电气化进程应该重视区域的协调发展,避免高电气化产业在某一地区过于集中[23]。
| 表 5 SDM模型的效应分解 |
碳排放强度控制是我国实现碳达峰和碳中和的主要制度。电气化对碳排放强度的两个决定因素(碳排放和经济增长)都有重要影响,但是二者之间的关系特征尚不明朗。在这个背景下,本文根据电气化与碳排放强度关系的现有研究,提出了电气化与碳排放强度之间可能存在EKC关系的两个假设,并通过面板模型和空间计量模型对其进行了检验。
结果显示,本文提出的H1和H2两个假设均成立。无论是否考虑空间因素,电气化与碳排放强度之间都存在显著的EKC关系,即随着电气化水平的提高,碳强度先上升后下降。在不考虑空间因素时,倒U形EKC的拐点位于电气化为10.52 % 的位置。这一拐点在纳入空间因素的分析中略微后移到10.81 % 的位置。从EKC拐点与目前中国电气化水平的关系来看,截至2016年,所有省份均已经处于EKC拐点右侧。需要指出的是,本文使用了中国30个省级层面(未包括西藏及港澳台地区)的面板数据,那么碳排放强度关于电气化EKC的拐点实际是全国层面的平均拐点。因此,对于辽宁(13.6 %)、吉林(13.5 %) 和黑龙江(13.5 %)这三个电气化水平较低的地区来说,仍然存在着碳排放强度随电气化水平提高而提高的风险。
根据上述结论,本文提出以下建议:首先,提高推动电气化的政策力度,充分利用电气化降低碳排放强度的效益。进一步出台相应电能替代激励政策,落实“十四五”规划中指出的“以碳强度控制为主”的低碳转型制度,并且注意在推进东北地区电气化进程时,要充分发挥其风力资源丰富的优势,增加非化石能源电力对电气化的贡献,尽量避免电气化提高使碳排放强度上升的情况。其次,在配套设施上,要进一步优化跨省份跨区域输电通道布局,促进清洁能源在更大范围内的配置,为扩大电气化提供保障。充分利用新冠肺炎疫情后财政刺激带来的机遇,加速电气化基础设施建设,并着重于可再生电力的发展。再次,还应当建立区域间的协同机制,并保障政策的一致性,避免区域间电气化水平差异过大,防止电气化对碳排放强度造成空间上的负面影响。最后,在关注电气化发展的同时,还应该关注电力的低碳化。一方面要继续鼓励清洁能源增量的发展,另一方面要通过加速煤电机组退役对存量进行调控,使用以新能源为主体的清洁电力填补缺口,实现电气化与低碳化的同步发展。
| [1] |
王锋, 冯根福, 吴丽华. 中国经济增长中碳强度下降的省区贡献分解[J]. 经济研究, 2013, 48(8): 143-155. |
| [2] |
孙欣, 张可蒙. 中国碳排放强度影响因素实证分析[J]. 统计研究, 2014, 31(2): 61-67. DOI:10.3969/j.issn.1002-4565.2014.02.009 |
| [3] |
IEA. CO2 Emissions from Fuel Combustion 2020 Edition[R]. Paris: IEA, 2020.
|
| [4] |
IEA. World Energy Outlook 2020[R]. Paris: IEA, 2020.
|
| [5] |
IRENA. Global Energy Transformation: A Roadmap to 2050[R]. Abu Dhabi: IRENA, 2019.
|
| [6] |
王灿. 碳中和愿景下的低碳转型之路[J]. 中国环境管理, 2021, 13(1): 13-15. |
| [7] |
张贤, 郭偲悦, 孔慧, 等. 碳中和愿景的科技需求与技术路径[J]. 中国环境管理, 2021, 13(1): 65-70. |
| [8] |
HOFMANN J, GUAN D, CHALVATZIS K, et al. Assessment of electrical vehicles as a successful driver for reducing CO2 emissions in China[J]. Applied energy, 2016, 184: 995-1003. DOI:10.1016/j.apenergy.2016.06.042 |
| [9] |
LUH S, BUDINIS S, GIAROLA S, et al. Long-term development of the industrial sector-Case study about electrification, fuel switching, and CCS in the USA[J]. Computers & chemical engineering, 2020, 133: 106602. |
| [10] |
BELLOCCHI S, MANNO M, NOUSSAN M, et al. Electrification of transport and residential heating sectors in support of renewable penetration: Scenarios for the Italian energy system[J]. Energy, 2020, 196: 117062. DOI:10.1016/j.energy.2020.117062 |
| [11] |
THOMAßEN G, KAVVADIAS K, NAVARRO J P J. The decarbonisation of the EU heating sector through electrification: a parametric analysis[J]. Energy policy, 2021, 148: 111929. DOI:10.1016/j.enpol.2020.111929 |
| [12] |
PENG W, YANG J N, LU X, et al. Potential co-benefits of electrification for air quality, health, and CO2 mitigation in 2030 China[J]. Applied energy, 2018, 218: 511-519. DOI:10.1016/j.apenergy.2018.02.048 |
| [13] |
刘生龙, 高宇宁, 胡鞍钢. 电力消费与中国经济增长[J]. 产业经济研究, 2014(3): 71-80. |
| [14] |
周绍杰, 刘生龙, 胡鞍钢. 电力发展对中国经济增长的影响及其区域差异[J]. 中国人口·资源与环境, 2016, 26(8): 34-41. DOI:10.3969/j.issn.1002-2104.2016.08.006 |
| [15] |
李强, 王洪川, 胡鞍钢. 中国电力消费与经济增长——基于省际面板数据的因果分析[J]. 中国工业经济, 2013(9): 19-30. |
| [16] |
王绵斌, 张妍, 谢品杰, 等. 电力投资规模对经济发展的门槛效应研究——基于京津冀和长三角地区数据[J]. 价格理论与实践, 2018(11): 119-122. |
| [17] |
齐绍洲, 李杨. 可再生能源消费影响经济增长吗?——基于欧盟的实证研究[J]. 世界经济研究, 2017(4): 106-119. |
| [18] |
王帅. 中国能源使用绿色化、碳排放与经济增长的关系研究[J]. 软科学, 2020, 34(10): 7-11, 24-24. DOI:10.3969/j.issn.1003-2800.2020.10.002 |
| [19] |
林伯强. 电力消费与中国经济增长: 基于生产函数的研究[J]. 管理世界, 2003(11): 18-27. |
| [20] |
JIANG L, HE S X, ZHONG Z Q, et al. Revisiting Environmental Kuznets Curve for carbon dioxide emissions: the role of trade[J]. Structural change and economic dynamics, 2019, 50: 245-257. DOI:10.1016/j.strueco.2019.07.004 |
| [21] |
沈坤荣, 马俊. 中国经济增长的"俱乐部收敛"特征及其成因研究[J]. 经济研究, 2002(1): 33-39. |
| [22] |
朱平辉, 袁加军, 曾五一. 中国工业环境库兹涅茨曲线分析——基于空间面板模型的经验研究[J]. 中国工业经济, 2010(6): 65-74. |
| [23] |
郝宇, 廖华, 魏一鸣. 中国能源消费和电力消费的环境库兹涅茨曲线: 基于面板数据空间计量模型的分析[J]. 中国软科学, 2014(1): 134-147. DOI:10.3969/j.issn.1002-9753.2014.01.017 |
| [24] |
DING Y T, ZHANG M, CHEN S, et al. The environmental Kuznets curve for PM2.5 pollution in Beijing-Tianjin-Hebei region of China: a spatial panel data approach[J]. Journal of cleaner production, 2019, 220: 984-994. |
| [25] |
XIE Q C, XU X, LIU X Q. Is there an EKC between economic growth and smog pollution in China? New evidence from semiparametric spatial autoregressive models[J]. Journal of cleaner production, 2019, 220: 873-883. |
| [26] |
柏培文, 许捷. 中国三大产业的资本存量、资本回报率及其收敛性: 1978-2013[J]. 经济学(季刊), 2018, 17(3): 1171-1206. |
| [27] |
ANSELIN L, GRIFFITH D A. Do spatial effects really matter in regression analysis[J]. Papers in regional science, 1988, 65(1): 11-34. |
| [28] |
ANSELIN L, GETIS A. Spatial statistical analysis and geographic information systems[J]. The annals of regional science, 1992, 26(1): 19-33. DOI:10.1007/BF01581478 |
| [29] |
LESAGE J P. An introduction to spatial econometrics[J]. Revue d'économie industrielle, 2008, 123(3): 19-44. |
| [30] |
程叶青, 王哲野, 张守志, 等. 中国能源消费碳排放强度及其影响因素的空间计量[J]. 地理学报, 2013, 68(10): 1418-1431. DOI:10.11821/dlxb201310011 |
| [31] |
陈诗一. 中国碳排放强度的波动下降模式及经济解释[J]. 世界经济, 2011, 34(4): 124-143. |
| [32] |
ZHAO X G, LU F. Spatial distribution characteristics and convergence of China's regional energy intensity: an industrial transfer perspective[J]. Journal of cleaner production, 2019, 233: 903-917. |
 2021, Vol. 13
2021, Vol. 13