长江经济带横跨我国东、中、西三大板块,同时人口数量和生产总值在我国占比均在40%以上,在我国经济发展中扮演着重要角色。但是,随着工业化和城镇化的高速发展,长江经济带面临严重的资源环境问题。一方面,水资源利用效率低,工业用水需求不断增加;另一方面,工业废水排放量不断增加,长江水环境承载力面临较大压力。2016年出台的《长江经济带发展规划纲要》以及2017年出台的《长江经济带生态环境保护规划》都指出长江经济带要坚持走“生态优先、绿色发展”的道路,2018年4月习近平总书记主持召开第二次长江经济带发展座谈会,再次强调“共抓大保护,不搞大开发”,更是要求在发展的同时,坚守绿色底线,抓好生态文明建设,从而实现经济发展与生态保护和谐共生。在此背景下,研究长江经济带工业用水效率问题,有利于实现水资源的优化配置,促进长江经济带高质量绿色发展。
1 文献综述如何提高工业用水效率,实现水资源的优化配置,已经成为社会可持续发展的重要问题之一,提高工业用水效率势在必行。常见的水资源效率测度方法有随机前沿分析法(Stochastic Frontier Analysis,SFA)[1]、数据包络分析法(Data Envelopment Analysis,DEA)[2]等。在SFA方面,雷贵荣等[3]构建SFA节水测算模型来反映徐州市工业用水的动态变化特征,得出徐州市工业用水效率不断上升的结论。陈关聚和白永秀[4]使用SFA方法得出2003—2010年我国31个省份工业全要素用水效率在逐年提升的结论。雷玉桃和黄丽萍[5]运用SFA方法测算了我国工业用水效率,并进行了东、中、西区域效率差异分析,结果表明,三个地区间差异明显,东部工业用水效率最高,中部次之,西部工业用水效率最低。
由于DEA方法可以避免SFA法函数形式的设定错误造成的计算问题[6],更多的学者采用的是DEA方法,并在传统DEA模型上不断改进。在传统DEA方面,Hu等[7]在DEA方法基础上,首次定义了“全要素用水效率”,发现用水效率随人均收入出现先降低后上升的趋势,此后,DEA方法被广泛应用于水资源效率研究中。程永毅和沈满洪[8]将地区要素禀赋的投入价格体系纳入DEA模型,测算得出我国大部分地区工业用水效率并未表现出较强的收敛趋势。卢曦和许长新[9]剔除了环境因素和随机误差因素,采用三阶段DEA和Malmquist指数相结合的方式,对长江经济带的用水效率进行了动态和静态的分析。
传统DEA模型存在忽略非径向松弛变量的缺点[10]。基于此,Tone[11]提出了非径向的SBM(Slack Based Measure)模型,考虑所有径向与非径向松弛的变量,受到学术界的广泛认可。李静和马潇璨[12]采用SBM模型指出在考虑工业水污染后,中国各省份工业用水效率普遍较低。Wang等[13]将氨氮排放量和化学需氧量作为非期望产出,利用SBM-DEA模型测算出各省份工业用水效率,发现工业用水效率存在显著的地理差异。赵良仕等[14]将工业用水利用分成水资源利用和污染物处理两阶段,利用SBM模型测度我国31个省级行政区的水资源利用整体效率,并利用空间自相关分析法分析工业用水效率的时空特征。邓光耀和张忠杰[15]利用网络SBM-DEA模型测算我国各省份工业用水效率,并利用GML指数分析影响用水效率的原因。
SBM模型缺少了投入或是产出目标值与实际值之间的比例信息,得出的效率值通常会低于实际效率值。为解决这一问题,Tone和Tsutsui[16]提出了EBM(Epsilon-Based Measure)模型,该模型是一种混合模型,同时包含径向与SBM两类距离函数,为评价决策单元效率提供了一种新方法。张玮和刘宇[17]将水资源利用过程作为影响因素,利用EBM模型测度长江经济带绿色水资源效率。肖磊等[18]利用超效率EBM模型测算中国30个省份的工业用水效率,并利用基尼系数和空间计量模型分析工业绿色水资源效率的差异和收敛性。
总的来说,目前国内外学者在测算工业用水效率的空间差异和影响因素方面取得了一定的成果,但在测算方法和指标选择上存在一定的局限性。一方面已有文献在研究工业用水效率时大多使用径向或是非径向距离函数测算效率值,往往导致效率值不准确。另一方面已有文献通常选用工业废水作为非期望产出来计算工业用水的效率,忽略在工业废水治理方面的费用投入。因此,本文将EBM模型应用于工业用水效率领域,可以融合径向和非径向距离函数,使效率值更加准确。同时,将工业废水治理费用作为一项投入变量,遵循“越少越优”的原则,纳入投入指标体系中。进而,利用泰尔(Theil)指数对长江经济带工业用水效率存在时空差异的原因进行分析,并利用Tobit模型分析影响工业用水效率的因素以期为推动长江经济带工业经济绿色发展提供政策建议。
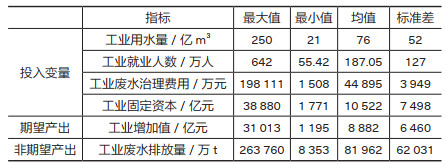
2 数据来源与模型构建 2.1 变量选择与数据来源本文选用长江经济带9省2市作为决策单元,同时进一步划分为上游、中游与下游三大地区,其中上游地区包括重庆市、四川省、云南省与贵州省,中游地区包括安徽省、江西省、湖北省与湖南省,下游地区包括上海市、江苏省与浙江省。考虑数据的可得性,本文以各省(市)工业用水量、工业就业人数、工业固定资本和工业废水治理费用作为投入指标,各省(市)工业增加值作为期望产出指标(按照出厂价格指数将其折算为2007年不变价格),工业废水排放量作为非期望产出指标。各指标变量数据来自2008— 2018年《中国统计年鉴》《中国环境统计年鉴》并经整理得到。投入产出变量描述性统计如表 1所示。
| 表 1 2007—2017年长江经济带投入产出变量描述性统计 |
本文选用的EBM模型,可以克服SBM模型的弊端,兼容径向与非径向松弛变量,反映实际值与目标值之间的比例信息。EBM模型强调在产出不变的条件下,衡量各投入量的变化情况,以此来测度其效率值。假设有N个决策单元(Decision Making Unit,DMU),记为DMUj(j=1,2,...,N);每个DMU有M种投入,记作xi(i=1,2,...,M);s种产出,记作yr(r=1,2,...,s);X={xij}∈RM×N,Y={yij}∈RM×N分别是投入和产出矩阵,且X>0,Y>0;那么测量长江经济带的工业用水效率的EBM模型的方程式为:
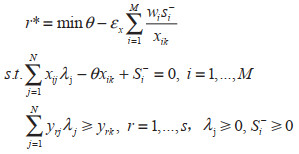
|
(1) |
式(1)中,r*是不考虑非期望产出的效率值,满足0≤r*≤1;xik和yrk是决策单元k的第i种投入和第r种产出;θ是径向模型测出的效率值;M是投入指标个数;Si−是各投入指标的松弛变量,由达到最优前沿面时的目标值于原始值的差距决定;wi是各投入指标的权重,表示相对重要程度;λ是决策单元的线性组合系数;εx是结合径向θ和非径向松弛的关键参数,取值范围是[0, 1],取0时相当于径向模型,取1时相当于SBM模型。式(1)的解是长江经济带各省(市)的综合技术效率,若添加∑ λ=1的约束条件,可以求解长江经济带各省(市)工业用水的纯技术效率,二者的比值即为规模效率。
EBM模型计算过程如下:
(1)通过SBM模型得到的各项投入指标的投影向量xf,f=1,2,...,i,j,...,m。
(2)设S (xi, xj)和D (xi, xj)为xi、xj两个向量间的关联指数和离散指数。
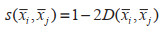
|
(2) |
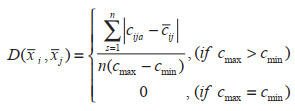
|
(3) |
其中,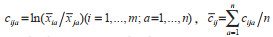
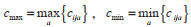
(3)利用建立的关联指数矩阵,计算EBM模型的参数。
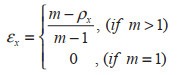
|
(4) |
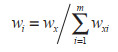
|
(5) |
为了表达方便,文中基于投入导向、规模报酬不变的EBM模型简写为EBM-I-C,基于投入导向、规模报酬可变的EBM模型简写为EBM-I-V。
2.3 泰尔指数及分解本文使用泰尔指数(Theil Index)来测度工业用水效率差距程度,并基于泰尔指数的分解方法,将差异分解成区域内差异和区域间差异,并对差异结构进行分析。泰尔指数公式如下所示:
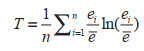
|
(6) |
其中,T是测度工业用水效率差距程度的泰尔指数;ei表示i省(市)的工业用水效率;e表示长江经济带11个省份的平均工业用水效率。
泰尔指数作为工业用水效率的测度指标具有良好的可分解性质。假定n个个体的样本被分成K个群组,每组分别为gk(k=1,...,K),第k组gk中的个体数目为nk,则有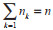
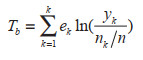
|
(7) |
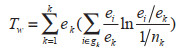
|
(8) |
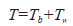
|
(9) |
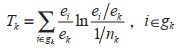
|
(10) |
进一步地,可以计算第K组组内的贡献率Dk和组间差距的贡献率Db分别为:
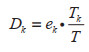
|
(11) |
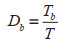
|
(12) |
为了分析长江经济带工业用水效率时空差异的影响作用机制,需要对相关影响因素进行检验。由于长江经济带的工业用水效率值处在[0, 1]之间,属于双截尾变量,如果采用普通OLS会导致参数估计量产生有偏性和不一致性,因此本文选择Tobit回归模型。模型具体如下所示:
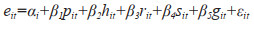
|
(13) |
式中,eit是长江经济带i省(市)每年的工业用水效率;αi是常数项;pit、hit、rit、sit、git是长江经济带各年各省(市)的经济发展水平、工业化程度、技术水平、水资源禀赋和政府环境管制力度;β1、β2、β3、β4、β5是待求系数;εit是随机项。
3 实证结果及分析 3.1 工业用水效率的时空差异以往研究显示,决策单元的数量会影响测度效率的准确性[19]。为避免决策单元较少和数据稀疏而导致效率差异性过低,本文采用窗口分析方法对决策单元进行测度,设定窗口宽度为2,也就是说每一年的效率值由当年和往年的投入产出值共同决定,因此效率计算时间为2008—2017年。具体结果如图 1所示。
|
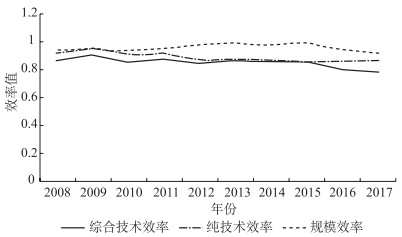
图 1 2008—2017年长江经济带整体工业用水综合技术效率、纯技术效率与规模效率 |
从图 1可以看出,2008—2017年长江经济带整体工业用水综合技术效率一直低于1,工业用水效率存在提升空间。在2008—2011年工业用水效率波动上升,工业用水效率较高,但自2011年以来长江经济带整体工业用水效率值波动下降,说明近年来长江经济带在追求工业经济发展的过程中,忽视了控制工业废水排放,导致了工业经济与环境之间发展不协调的情况出现。
从效率分解结果来看,在2010—2017年,规模效率一直高于纯技术效率,且在2008—2017年纯技术效率的波动是工业用水综合技术效率波动的主要原因,这说明各工业部门在控制工业用水规模的同时,也要注重提高工业废水处理技术,减少工业废水的排放及提高工业废水的利用效率。
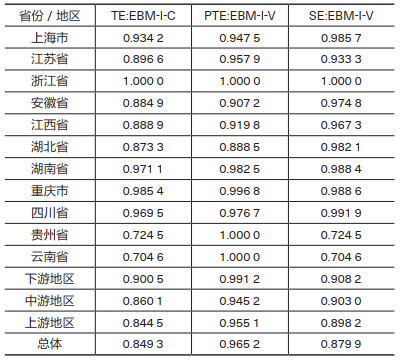
从表 2结果来看,长江经济带下游地区综合效率数值最高,说明下游地区单位工业产值带来的水资源环境压力较小;长江上游地区的4个省市效率均值最低,工业用水效率亟待提升。省际层面上,浙江省的工业用水是完全有效率的,四川省和重庆市位居第二、三位;云南省和贵州省工业用水的效率较低,均在0.8以下,表明工业用水、工业废水治理和工业增加值之间的关系不平衡。
| 表 2 长江经济带工业用水效率值 |
从分解结果来看,在纯技术效率水平方面,长江下游地区的3个省市纯技术效率平均水平是0.9912,均值较高,表明这3个省市的工业用水技术和废水处理技术都处于领先水平。长江中游地区的纯技术效率最低,长江中游地区是传统老工业基地,资源型产业密集,工业技术落后,工业污染严重。在省际方面,长江上游的云南省和贵州省的表现都很突出,表明长江上游地区节水型社会建设取得了进步,污染产出相对较小。
在规模效率水平方面,长江上游地区工业用水规模效率数值在三个地区中最低,这就说明了上游地区要在投入成本和工业水资源利用之间进行合理分配。长江下游地区的工业用水规模效率为0.9082,在三个地区中效率最高,说明长江下游地区工业水资源利用和水污染排放规模较为合理。此外,在省际层面,浙江省实现了完全有效率,实现了工业用水与工业增加值的最佳规模;江苏省的工业用水效率值为0.9333,明显偏低,结合江苏省的统计数据来看,江苏省的工业用水总量是最高的,由于边际报酬递减规律,资源投入过多会造成规模效益减少,导致工业用水效率下降。江苏省要控制投入,避免投入过多造成效率下降。而贵州省与云南省的工业用水规模效率为0.7245和0.7046,远远落后于长江经济带其他省市,云、贵两地经济发展水平落后,地区工业规模落后于其他省市。因此,要扩大工业规模,充分发挥规模经济的优势,提高规模效率。
3.2 工业用水效率地区差距的形成原因长江经济带的工业用水效率存在空间差异,本节利用Matlab软件计算泰尔指数来诠释长江经济带各区域的效率值差距形成原因,将地区总体差距分为地区间差距和地区内部差距,并衡量二者对总体差距的贡献率。
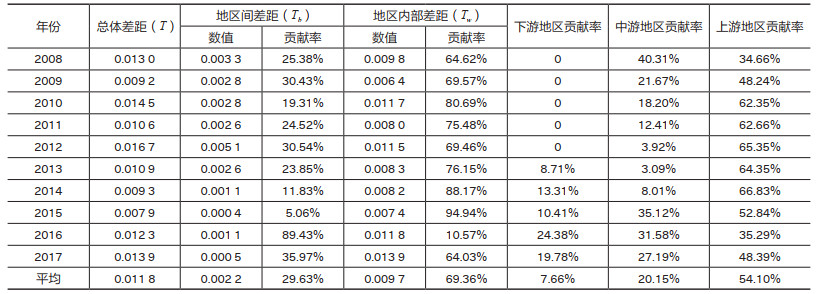
如表 3所示,2008—2017年长江经济带工业用水效率值地区差距的泰尔指数T是波动上升的,从2008年的0.0130波动上升至2017年的0.0139,累计增幅0.06%。这表明长江经济带工业用水效率的地区差距在扩大。从泰尔指数分解结果来看,地区内部差距贡献率(Tw)的均值69.36%要高于地区间差距贡献率(Tb)的均值29.63%,故地区内部差距是造成长江经济带工业用水效率值地区差距的主要原因,这表明政府应将缩小地区内部差距作为缩小工业用水资源效率总体差距工作的重点。
| 表 3 2008—2017年长江经济带地区间差距及内部差距对工业用水效率总体差距的贡献率 |
从三大区域内部差距Tw贡献率来看,长江上游地区贡献率最大,均值为54.10%。云、贵两地工业用水规模效率低,与川、渝两地差距大。长江上游地区内部差异大是造成长江经济带区域内部差距的主要原因。从时间变化来看,长江下游地区的贡献率近年来有上升的趋势,主要是江苏工业用水规模效率的下降所致。中游地区的贡献率处于居中位置,区域内各省市工业用水效率差异较小。上游地区的贡献率呈波动下降趋势,说明近年来上游地区节水型社会建设工作取得了一定成绩。
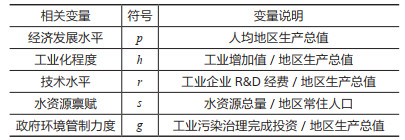
3.3 长江经济带工业用水效率影响因素分析在兼顾数据可得性的基础上,本文选取经济发展水平、工业化程度、技术水平、水资源禀赋和政府环境管制力度等5个代表性的指标对长江经济带及三大区域工业用水效率进行分析。相关影响因素的选取和说明详见表 4,数据来源于2009—2018年各省份《统计年鉴》《中国环境统计年鉴》及国家统计局官网。
| 表 4 长江经济带工业能源环境效率影响因素的选取及其说明 |
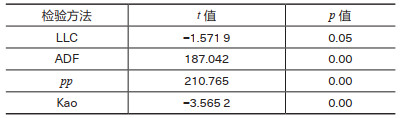
首先,从表 5可以看出通过LLC法和ADF Fisher法对面板数据进行单位根检验,p值为0.05和0.00,均小于0.1,所以数据全部通过单位根检验。其次,利用Kao检验对面板数据进行协整检验,p值为0.00,通过协整检验,表明面板数据可以进行Tobit模型回归分析。
| 表 5 单位根及协整检验结果 |
最后,对面板模型进行了Hauseman检验,p值为0.00,说明在5%的显著性水平下拒绝原假设,模型应为固定效应面板模型。本文通过stata12.0软件,利用固定面板Tobit模型得到2008—2017年长江经济带整体及各区域工业用水效率影响因素的回归结果,如表 6所示。
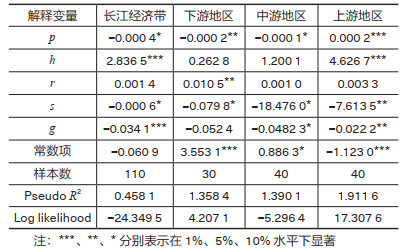
| 表 6 长江经济带及三大地区回归结果 |
根据表 6,各影响因素的实证结果分析如下:
(1)经济发展水平角度。就长江经济带上游地区而言,经济发展水平与工业用水效率呈正相关,经济发展水平的提高有利于提高长江经济带的工业用水效率。长江经济带上游地区经济发展水平回归系数是0.0002,即在其他条件不变下,人均GDP每增加1%,工业用水效率提升0.0002%。经济水平的提高,可以为工业用水效率提供财政和技术支持,从而提高工业用水效率。长江经济带整体和长江下游、中游地区经济发展水平回归系数为负,经济发展水平与工业用水效率呈负相关。长江下游和中游相较于上游而言,经济发展速度较快,但发展的同时也对水资源和水环境带来了负面影响。
(2)工业化程度角度。工业化程度提高对长江经济带整体工业用水效率有正向作用。就三个地区来看,工业化程度对上游地区的影响最大,上游地区工业发展迅速,产业集聚效果明显,工业用水效率提升明显。工业化程度变化对长江下游、中游地区影响不显著,中游和下游地区第二产业比重基本稳定,工业化强度增加对提升工业用水效率作用微小,应重点优化工业行业内部结构,减少高耗水、高废水的企业。
(3)技术水平角度。技术水平对长江经济带整体及各地区工业用水效率的提高有正向作用。长江经济带整体技术水平的系数为0.0014。增加规模以上工业企业R & D投入占GDP的比重对中游和上游地区影响不显著。究其原因,与长江中游和上游相比,下游地区的工业用水技术,工业废水处理技术与工业生产联系密切,当R & D投入增加时,工业企业会转化到生产过程中,促进技术效率的提高;中游和上游地区受限于基础设施和技术水平,转化速度较慢。
(4)水资源禀赋角度。水资源禀赋的系数都为负,说明水资源禀赋增加,工业用水效率降低。从长江经济带整体回归结果来看,水资源禀赋系数为负,表明二者之间是负相关关系原因可能在于节水意识淡薄,在工业生产领域方面导致产出不变的前提下水资源过度利用。
(5)政府环境管制力度角度。从回归结果来看,长江经济带三大地区政府环境管制力度的回归系数为负,政府环境管制力度与工业用水效率之间是负相关,政府环境管制力度的加强并没有促进工业用水效率的提升。可能是由于我国目前的排污收费制度不完善,一些企业在落实污染收费制度的时候,污染治理成本过高而放弃升级改造企业生产线,主动认缴罚金,未达到理想效果。此外,长江经济带的工业企业正处于绿色转型换代中,绿色改造技术不完善,严格的环境政策会降低长江经济带工业产值。但从长期来看,当长江经济带工业企业完成了绿色转型形成经济产出时,工业用水效率将提升到一个新的水平。
4 结论与建议 4.1 主要结论本文通过构建EBM模型来测算长江经济带各省(市)的工业用水效率,同时构建Tobit面板模型对长江经济带整体和上游、中游和下游地区影响因素进行了分析,得出以下结论:
(1)工业用水综合技术效率波动下降,纯技术效率波动下降是主要原因。在追求工业发展的过程中,总体工业用水效率水平较低,忽视工业用水技术及废水处理技术的提升,造成工业发展与资源环境之间的不平衡。
(2)从效率分解结果来看,不同地区面临着不同难题。长江上游地区纯技术效率水平较高,规模效率较低;长江中游地区纯技术水平效率较低,规模效率较高;长江下游地区如江苏省,是长江经济带纯技术效率方面表现优秀的省份,但由于消耗过多资源,已进入边际报酬递减阶段,规模效率表现不佳。
(3)不同影响因素对长江经济带不同地区影响不同。经济发展水平对上游地区提高工业用水效率作用显著,但对中游和下游地区效果不佳。工业化程度对上游地区效果十分显著,对中游和下游地区工业用水效率影响较小。中上游地区由于生产技术水平和基础设施落后,工业用水效率对R & #38;D的增加反应不敏感。水资源禀赋增加会使三个地区的工业用水效率降低。政府管制力度增强同样也会降低三个地区工业用水效率。
4.2 政策建议(1)各级政府应重视提高工业用水技术水平,促进工业生产与技术紧密结合。应积极提高工业行业技术水平,增加对工业用水技术的投资。应开发工业用水循环利用设备,降低万元工业增加值工业用水量,同时提高工业废水处理技术水平,降低在工业生产过程中产生的工业废水。
(2)根据不同区域的情况,应加强建设的针对性,制定因地制宜的政策。对于上游地区来说,要扩大工业规模,发挥规模效率递增的作用来提高工业用水效率。对于中游地区来说,要鼓励工业企业进行自我创新、工艺革新,提高资源的利用效率,降低废水排放率。对于下游地区的江苏来说,在控制工业规模的同时,要提高工业技术水平,减少工业规模不经济的负面影响。
(3)提高工业用水效率是综合的系统工程,应采取多种措施来提高工业用水效率。应加快长江上游地区经济发展水平,提高上游地区工业化程度,发挥经济发展与工业化程度对提高工业用水效率的正向积极作用,继续增加对中上游地区工业企业的科研投入。对整个长江经济带来说,应提高公民的节水环保意识,加大环保执法力度,增加工业污染治理投资,完善排污许可制度和污染收费制度,实施动态管理和环境监测,充分发挥污染治理投资的积极作用。
| [1] |
KANEKO S, TANAKA K, TOYOTA T, et al. Water efficiency of agricultural production in China:Regional comparison from 1999 to 2002[J]. Archives of virology, 2000, 145(5): 859-869. |
| [2] |
SPEELMAN S, D'HAESE M, BUYSSE J, et al. Technical efficiency of water use and its determinants, study at small-scale irrigation schemes in North-West Province, South Africa[C]//106th EAAE Seminar. Montpellier, France, 2007.
|
| [3] |
雷贵荣, 胡震云, 韩刚. 基于SFA的工业用水节水潜力分析[J]. 水资源保护, 2010, 26(1): 66-69. |
| [4] |
陈关聚, 白永秀. 基于随机前沿的区域工业全要素水资源效率研究[J]. 资源科学, 2013, 35(8): 1593-1600. |
| [5] |
雷玉桃, 黄丽萍. 中国工业用水效率及其影响因素的区域差异研究——基于SFA的省际面板数据[J]. 中国软科学, 2015(4): 155-164. |
| [6] |
CHARNES A, COOPER W W, RHODES E. Measuring the efficiency of decision making units[J]. European journal of operational research, 1978, 2(6): 429-444. |
| [7] |
HU J L, WANG S C, YEH F Y. Total-factor water efficiency of regions in China[J]. Resources policy, 2006, 31(4): 217-230. |
| [8] |
程永毅, 沈满洪. 要素禀赋、投入结构与工业用水效率——基于2002-2011年中国地区数据的分析[J]. 自然资源学报, 2014, 29(12): 2001-2012. |
| [9] |
卢曦, 许长新. 基于三阶段DEA与Malmquist指数分解的长江经济带水资源利用效率研究[J]. 长江流域资源与环境, 2017, 26(1): 7-14. |
| [10] |
ZHOU P, ANG B W, WANG H. Energy and CO2 emission performance in electricity generation:a non-radial directional distance function approach[J]. European journal of operational research, 2012, 221(3): 625-635. |
| [11] |
TONE K. A slacks-based measure of efficiency in data envelopment analysis[J]. European journal of operational research, 2001, 130(3): 498-509. |
| [12] |
李静, 马潇璨. 资源与环境双重约束下的工业用水效率——基于SBM-Undesirable和Meta-frontier模型的实证研究[J]. 自然资源学报, 2014, 29(6): 920-933. |
| [13] |
WANG Y S, BIAN Y W, XU H. Water use efficiency and related pollutants' abatement costs of regional industrial systems in China:a slacks-based measure approach[J]. Journal of cleaner production, 2015, 101: 301-310. |
| [14] |
赵良仕, 孙才志, 刘凤朝. 环境约束下中国省际水资源两阶段效率及影响因素研究[J]. 中国人口 & #183;资源与环境, 2017, 27(5): 27-36. |
| [15] |
邓光耀, 张忠杰. 基于网络SBM-DEA模型和GML指数的中国各省工业用水效率研究[J]. 自然资源学报, 2019, 34(7): 1457-1470. |
| [16] |
TONE K, TSUTSUI M. An epsilon-based measure of efficiency in DEA:A third pole of technical efficiency[J]. European journal of operational research, 2010, 207(3): 1554-1563. |
| [17] |
张玮, 刘宇. 长江经济带绿色水资源利用效率评价——基于EBM模型[J]. 华东经济管理, 2018, 32(3): 67-73. |
| [18] |
肖磊, 李云, 陈佳蕊. 中国工业绿色水资源效率的区域差异与收敛性研究[J]. 数量经济研究, 2020, 11(2): 133-149. |
| [19] |
王群伟, 周鹏, 周德群. 我国二氧化碳排放绩效的动态变化、区域差异及影响因素[J]. 中国工业经济, 2010(1): 45-54. |
 2020, Vol. 12
2020, Vol. 12